More Exam 2 Practice

Problem 1

The grade distribution for Professor Jones' Math 113 courses is as follows: 14% A, 39% B, 24% C, 5% D, 16% W.

1. Write a probability distribution for the grades in Math 113.

A probability distribution is a list of all the values the random variable can assume with their associated probabilities. The only probability not given is for an F and since the sum of the probabilities must be 1, we can determine the probability of getting an F by adding up the other probabilities and subtracting from 1.

A	B	C	D	F	W
0.14	0.39	0.24	0.05	0.02	0.16

2. A student is randomly selected from the course. Find the probability that he or she receives ...

Once the table is completed, these become fairly easy.

a. an F

P(F) = 0.02

b. an A or B

P(A or B) = P(A) + P(B) = 0.14 + 0.39 = 0.53

c. anything but a W

P(W') = 1-P(W) = 1 - 0.16 = 0.84

3. Three randomly selected students are chosen. Find the probability that ...

a. All three receive a B

P(BBB) = 0.39 (0.39) (0.39) = 0.059319

b. All of them pass with a C or better

The probability of any one student getting an A, B, or C is P(A, B, or C) = 0.14 + 0.39 + 0.24 = 0.77.

The probability of all three students getting that is 0.77 (0.77) (0.77) = 0.456533.

c. No one receives a C

The probability that any one student will not receive a C is P(C') = 1 - P(C) = 1 - 0.24 = 0.76.

The probability that all three students will not receive C's is P(C'C'C') = 0.76 (0.76) (0.76) = 0.438976

d. At least one of them withdraws (W)

The easiest way to work this is to realize that "at least one" is the complement of "none".

P(at least one withdrawal) = 1 - P(no withdrawals)

The probability of any one student not withdrawing is P(W') = 1 - P(W) = 1 - 0.16 = 0.84

The probability of all three students not withdrawing is P(No withdrawals) = 0.84 (0.84) (0.84) = 0.592704

The probablity of at least one withdrawal is 1 - 0.592704 = 0.407296

e. The third student is the only one to get an A

The first two students can not get an A, while the last one must.

The probability of any one student not getting an A is P(A') = 1 - P(A) = 1 - 0.14 = 0.86.

The probability we're looking for is P(A'A'A) = 0.86 (0.86) (0.14) = 0.103544

Problem 2

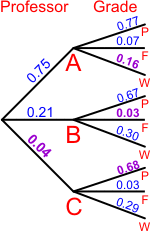
Three professors have taught Math 113 at Richland since 1997.

• Professor Alpha teaches 75% of the students and 77% of his students pass with a C or better, 7% get a D or F, and the rest withdraw.
• Professor Bravo teaches 21% of the students and 67% of his students pass with a C or better, 30% withdraw, and the rest get a D or F.
• Professor Charlie teaches the rest of the students and 3% of his students get a D or F, 29% withdraw, and the rest pass with a C or better.

Abbreviate the professor's names with A, B, or C. Let event P be passing with a C or better, event F be getting a D or F, and event W be withdrawing from the course.

1. Create a tree diagram depicting this situation. Completely and correctly label the tree diagram.

The probabilities that weren't given can be found because the sum of the probabilities for each event must be 1. On the tree diagram, the numbers you had to compute are shown as bold purple numbers where the supplied numbers are given in blue.

The distribution of grades depends on who the teacher is, so the professor comes first in the tree diagram and the grade comes second.

Tree diagram

2. Use the tree diagram to complete the joint probability table. Write all probabilities as decimals with four decimal places.

A joint probability is the probability when both events occur, that is, what they have in common. You find them by multiplying the probabilities along the branches of the tree diagram.

For example, since professor Alpha teaches 75% of the students and 77% of his students get a C or better, then the probability of a randomly selected student both having professor Alpha and passing with a C or better is 0.75 (0.77) = 0.5775

	A, B, or C	D or F	W	Total
Alpha	0.5775	0.0525	0.1200	0.7500
Bravo	0.1407	0.0063	0.0630	0.2100
Charlie	0.0272	0.0012	0.0116	0.0400
Total	0.7454	0.0600	0.1946	1.0000

3. Use the joint probability table to find the probabilities of the following.

Remember that we're calling A, B, or C event P, a D or F event F, and a W event W.

a. That a student had Professor Alpha and passed with a C or better.

This is a joint probability because of the "and". There is no prior knowledge, nothing is given, we need them both happen at the same time.

P(A and P) = 0.5775

b. That a student had Professor Bravo and withdrew.

P(B and W) = 0.0630

c. That a student received a D or F in the class.

This is a marginal probability. Only one category is referred to, the instructor isn't referenced at all. This is the total probability of getting a D or F.

P(F) = 0.0600

d. That a student passed with a C or better.

P(P) = 0.7454

e. That a student had Professor Alpha or passed with a C or better.

This contains the word "or" which means that we'll need to combine the categories, making sure we don't count any category more than once. In particular, if you take the total for professor Alpha and the total who get a C or better, you're looking at 0.7500 + 0.7454 = 1.4954, which cannot be a probability because probabilities have to be between 0 and 1 inclusive. We have to subtract the intersection of those two, which we double counted.

P(A or P) = P(A) + P(P) - P(A and P) = 0.7500 + 0.7454 - 0.5775 = 0.9179

f. That a student had Professor Alpha or Professor Bravo.

These two events don't overlap, so we don't need to worry about the intersection.

P(A or B) = P(A) + P(B) = 0.75 + 0.21 = 0.96

g. That a student who passed with a C or better took Professor Bravo.

This is a conditional probability. We know the student passed with a C or better. We're looking for the probability that one of those students took Professor Bravo.

This question could be worded in the following ways.

What is the probability that a student who passed with a C or better took Professor Bravo (this is the way it was worded)?
What percent of those students who passed with a C or better had Professor Bravo for an instructor?
A student passed with a C or better. What is the probability that he or she had Professor Bravo?

Here's how to work it out.

The probability of a student passing with a C or better is P(P) = 0.7454. Limit yourself to just those students.
Now, out of those students, what portion had Professor Bravo? This is P(B and P) = 0.1407.
Now divide Professor Bravo's part by all of those who passed with a C or better.

P(B|P) = P(B and P) / P(P) = 0.1407 / 0.7454 = 0.1888

h. That a student who withdrew took Professor Alpha.

This time, we know the student withdrew. We're looking for the probability that they took Professor Alpha.

P(A|W) = P(A and W) / P(W) = 0.1200 / 0.1946 = 0.6166.

Now that sounds really bad, but you need to understand why it's true. Professor Alpha had the lowest withdrawal rate of any of the teachers at only 16% of the students. However, he taught 75% of the students so he also teaches a large percent of those who withdraw. Instead of saying that 61.66% of the withdrawals came from Professor Alpha, it would be better to reference the fact that this is a lower rate than the 75% of all students who take him.

i. That a student who withdrew passed with a C or better.

This time, we know that the student withdrew and we're trying to find the probability that they also passed with a C or better.

Well, since they withdrew, they couldn't pass with a C or better, so the probability is 0.

P(P|W) = P(P and W) / P(W) = 0 / 0.1946 = 0