Old versions of Minitab would not find the test statistic. This has been fixed in version 14.20, but go ahead and complete the tables by hand so that you understand the process better. Check yourself with Minitab.
A table is given. The table contains the expected frequency and a contribution to chi-sq. The contribution to chi-sq is the (obs-exp)2/exp row of the table.
At the bottom, you will get a line that contains the df, test statistic, and p-value.
There are three options available in Minitab for dealing with probability distributions.
Okay, so of those options, the cumulative probability is the one we need to use.
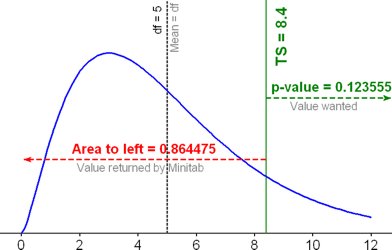
Here are the assumptions. We have a chi-square distribution with 5 df and the test statistic was 8.4. When we used Minitab to find the area to the right of 8.4, it returned 0.864475. Since this is a right tail test, we want the area to the right of 8.4 and since the entire area under the curve is 1, we can subtract the area of on the left from 1 to get the area on the right. That is 1 - 0.864475 = 0.123555. That's our p-value.

By the way, the figure above was generated using Minitab. I created a column of the numbers between 0 and 12, counting by 0.1, using the Calc / Make patterened data / Simple set of numbers command. I then went into Calc / Probability distributions / Chi-square and chose the Probability density function. My input column was the column with the numbers between 0 and 12 and I stored the probability values into another column. I then did a scatterplot and cleaned up and annotated the results.
Also note that I stopped at 12 because it showed most of the interesting features of the graph before 12. However, the graph continues on to the right forever, approaching the x-axis (the probabilities get really close to zero).