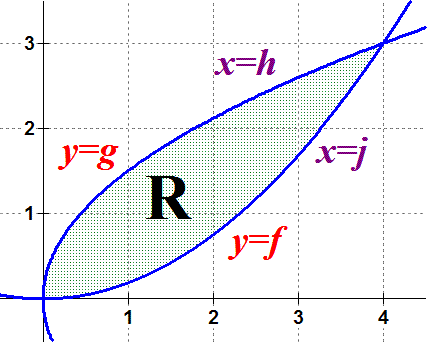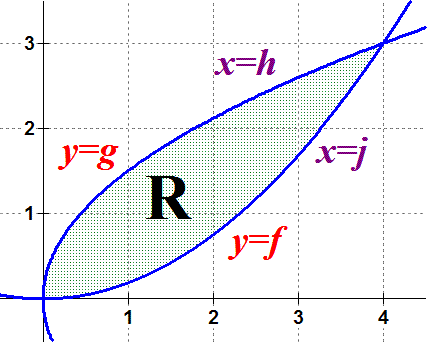Math 121: Chapter 5,7 Exam Study Guide
- A region is given with generic boundaries like y=f, y=g, x=h, x=k, etc. Write integrals that can be used to find the indicated values. Do not make any attempt to actually determine the functions or evaluate the integrals. Ten parts. Here are the different things you'll need to know.
- Area of the region in terms of both dx and dy
- Volume of rotation about a horizontal axis
- Volume of rotation about a vertical axis
- Length of a curve
- Surface area of revolution when a boundary is rotated about a horizontal axis
- Surface area of revolution when a boundary is rotated about a vertical axis
- Find the derivative. This involves mostly logarithms and exponential functions, but may involve logarithmic differentiation and implicit differentiation as well. Eight parts.
- Find the indefinite integral. This involves mostly logarithmic and exponential functions, but it may also include trigonometric functions that become possible to integrate once we have the logarithmic integral (like \(\int
\tan x\, dx = \ln | \sec x | + C \) ). Seven parts.
Notes
- There is no calculator allowed on the in-class portion of the exam.
- There is a take home exam worth 18 points that is due the day of the exam. The take home exam has 2 optional bonus questions at the end which will require that you read ahead in the text to answer.
Examples for Question 1
Use the following figure to write an integral that can be used to find the indicated value.
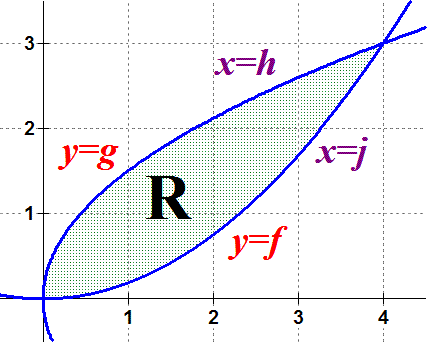
- Find the area of the region using an integral involving dx. Answer: \( \int_0^4 (g-f)\, dx \)
- Find the volume when the region is rotated about the x-axis. Answer: \( \int_0^4\pi \left(g^2 - f^2\right)\, dx \)
- Find the volume when the region is rotated about the y-axis. Answer: \( \int_0^4 2 \pi x (g - f)\, dx \) or \( \int_0^3 \pi \left (j^2 - h^2 \right)\, dy \)
- Find the length of the top portion between 1≤y≤3. Answer: \( \int_1^3 \sqrt {1 + (h')^2}\, dy \)
- Find the area of the surface generated by rotating the bottom curve about the x-axis. Answer \(
\int_0^4 2\pi f \sqrt { 1 + (f')^2 }\, dx\)
These are just some examples so you will have an idea what to expect. You also expect for the rotations to be about a non-axial line.
Chautauqua National Wildlife Refuge
This table contains the data needed for the Chautauqua National Wildlife Refuge problem on the take home exam. You should be able to copy/paste it into Excel (note that Firefox works best if you do not want to copy the formatting [borders and shading] with it).
23 measurements were taken along the north border and south border of the Refuge. The measurements were made each time the region had a vertex. All measurements are in kilometers.
| i |
east |
north |
south |
| 1 |
0.000 |
0.000 |
0.000 |
| 2 |
0.037 |
0.150 |
0.000 |
| 3 |
0.339 |
1.059 |
0.000 |
| 4 |
0.591 |
1.565 |
0.000 |
| 5 |
1.099 |
2.173 |
0.000 |
| 6 |
1.660 |
2.428 |
0.000 |
| 7 |
2.120 |
2.532 |
0.000 |
| 8 |
2.313 |
2.533 |
0.000 |
| 9 |
2.989 |
2.536 |
0.308 |
| 10 |
3.294 |
2.740 |
0.450 |
| 11 |
3.338 |
2.771 |
0.469 |
| 12 |
3.549 |
2.943 |
0.638 |
| 13 |
3.650 |
3.195 |
0.714 |
| 14 |
4.593 |
3.830 |
1.453 |
| 15 |
4.924 |
4.059 |
1.639 |
| 16 |
5.486 |
4.213 |
1.962 |
| 17 |
5.842 |
4.719 |
2.172 |
| 18 |
6.118 |
5.026 |
2.323 |
| 19 |
6.152 |
5.064 |
2.356 |
| 20 |
6.636 |
5.064 |
2.746 |
| 21 |
7.578 |
5.065 |
2.812 |
| 22 |
7.610 |
5.065 |
3.653 |
| 23 |
9.027 |
5.067 |
5.067 |
- i is the subscript for each point. They begin with i=1 on the far left (west) and go to i = 23 on the far right (east).
- east is the distance in kilometers east of the origin. You can think of it as the x-coordinate.
- north is the distance in kilometers north of the origin. You can think of it is as the y-coordinate of the top curve.
- south is the distance in kilometers south of the origin. You can think of it is as the y-coordinate of the bottom curve.
This region is from a shapefile downloaded from the National Atlas on November 15, 2012.
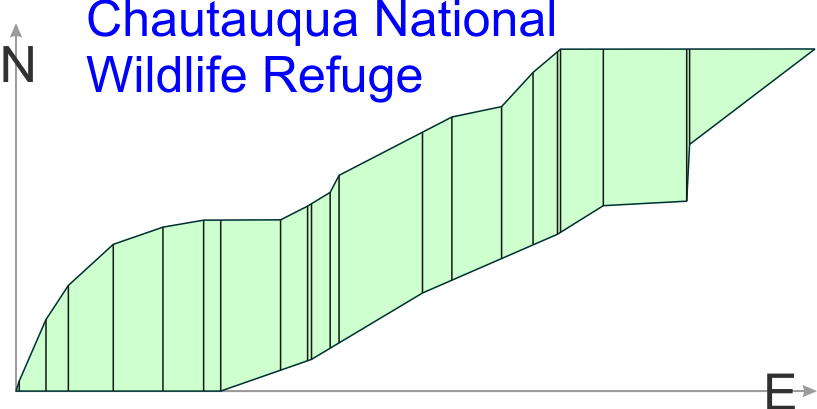
Note: In Excel, you can get ΔE by first typing DE, then highlighting just the D and changing the font to Symbol.
Points per problem
| # |
1 |
2 |
3 |
TH |
Total |
| Pts |
30 |
32 |
28 |
18+6 |
114 |