Project 3: Inverses

Instructions

Use Winplot and Google Docs to create a document with three problems on it. You may be able to locate similar problems in the book, but these problems should be your original creations.

Problem 1 - Graphing Inverses

1. Create a one-to-one function and pick a point on it where the derivative is not zero.
2. Find the instantaneous rate of change at the point.
3. Find the equation of the tangent line at that point.
4. Find the point on the inverse that corresponds to your original point.
5. Find the derivative of the inverse at that corresponding point.
6. Find the equation of the tangent line to the inverse at that corresponding point.
7. Create a graph that has: both functions (to graph the inverse, you can use Winplot to reflect the curve or graph it implicitly), the line y=x, both points, and both tangent lines.

Example Graph

You still need the answers to the other parts, but this is an example of what a graph might look like.

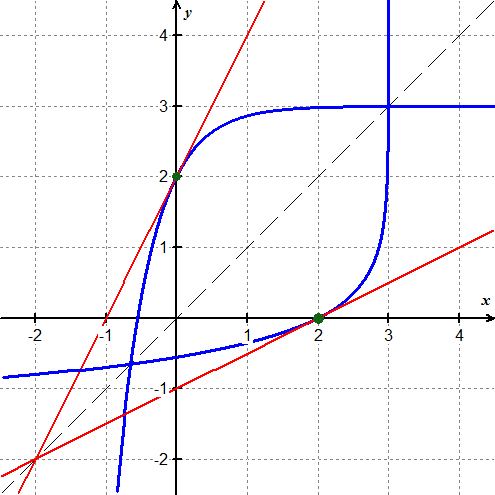
Problem 2 - Derivatives of Trigonometric Functions

Create 3 graphs, one for each pair of inverse trigonometric functions. Graph the inverse trigonometric function and its derivative. Then repeat the process for its cofunction. Develope and use a color scheme to illustrate that the inverse functions are symmetric about the line \( y=\frac{\pi}{4} \)and the derivatives of the inverse cofunctions are opposites of each other.

Problem 3 - Curve Fitting

Create problems that require fitting a curve to the given points. Provide a worked out solution with graph (to verify the solution) to the problem.

• Fit the function \( f(x) = A \ln x + B \) to two points (positive x values only)
• Fit the function \( f(x) = A e^{kx} + B \) to a y-intercept, a horizontal asymptote, and a second point.

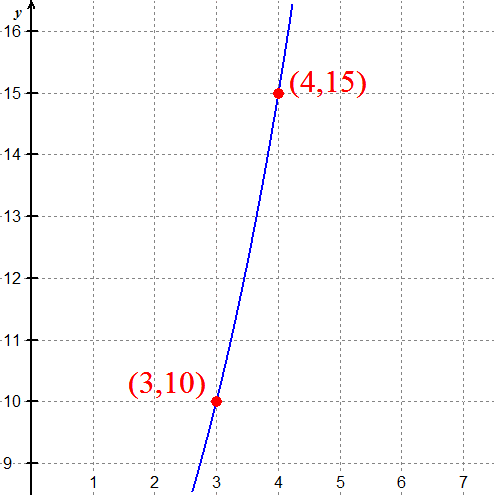
Example Problem

Find constants A and k so that the function \( f(x) = Ae^{kx} \) passes through (3,10), and (4,15).

Example Solution

You may find it easier to work the solution out on paper, take a picture with your cell phone, and upload that into Google Docs than to use the equation editor to type all this. Also note that I worked out the exact answers, most people go with decimal approximations. If you do this, wait until the end to round.

Substituting the points into the function gives: \( 10 = Ae^{3k} \) and \( 15 = Ae^{4k} \)

Divide those two equations to get \( \frac {15}{10} = \frac{Ae^{4k}}{Ae^{3k}} \), which simplifies to be \( \frac{3}{2} = e^k \).

Taking the natural logarithm of both sides gives \( k = \ln \frac 3 2 \).

Plugging that back into the first equation gives \( 10 = Ae^{3 \ln 3/2} = Ae^{(\ln 3/2)^3} = A \left ( \frac 3 2 \right )^3 \)

Solving for A yields \( A = 10 \left ( \frac 2 3 \right )^3 = \frac {80}{27} \).

The function is \( f(x) = \frac {80}{27} e^{x \ln 3/2} \).

You could also use decimal approximations to get \( f(x) = 2.96 e^{0.405 x} \).

Additional Notes

• Add your names at the top of the document under the title.
• Include instructions with each of the problems; don’t just create a graph or describe the graph.
• To submit the assignment, click the Share button in Google Docs and change it so that anyone with the link can view the results. Then copy the share link and email it to the instructor at james@richland.edu with an appropriate subject and the names of the people in the group. Only one person per group needs to submit the project.

Winplot Tips

File Menu

• When appropriate, use Image size to create a square document. The measurements are in centimeters. While 16.5 cm will make it fill the entire page horizontally, it will also take a lot of space vertically. You may want something smaller like 11.7 or 8.1, which will allow two side-by-side images.
• Use Bitmap to clipboard to capture the image so you can paste it into Google Docs. The regular copy to clipboard doesn’t work.
• Be sure to Save your graphic so that you can re-edit later if you need to do so.

Equa Menu

• Use implicit to graph an implicit equation. Sometimes, implicit graphs have a problem displaying if you change the zoom or arrow around to change the viewing. A workaround is to edit the graph in the inventory and then change the color.
• The inventory has a derive button that will graph the derivative of the selected function. The graph button will show or hide a graph, so a good way to make matching graphs is to sketch the function and derivative to make sure both are going to fit reasonably well on in the viewing window and then show one while hiding the other when you copy and paste the graph.

View Menu

• Use Grid to control the visibility of the grid, axes, tick marks, and labels. I recommend using a rectangular grid with dotted lines in all four quadrants. Check the scale box to show the numeric labels on the axes.
• Use View to control the domain and range of the image.

Btns Menu

• Use Text to add labels to the graph. Use the right mouse button to add or edit text and the left mouse button to drag it and change its position.

Google Docs Tips

Google Docs

• Increase the font size on your document. The equations are the size of your normal font, but that may be too small to see the mathematical expressions while editing them. You can change the font size and then update the Normal text style to match. Alternatively, you can highlight the entire document and change the font size, but this may not apply to text added later.
• Click the Share button at the top right and change who has access so that anyone with the link can view the document. Then you can just submit the link.

Equations

• Use Insert > Equation to insert an equation
• Create the structure before you use it. For example, click on the fraction template before typing the numerator.
• There are some keyboard shortcuts, most notably the ^ and _ give you superscripts and subscripts.
• Matrices are not supported. That might not sound like a big deal, but the trick to displaying piecewise functions is to create a matrix to use as placeholders. In fact, multi-line equations are not supported either. Basically, you don’t want to use Google Docs for serious mathematical content, but it will allow for collaboration.
• To get mathematical functions to display properly in an equation, precede them with a backslash. For example: sin x gives \( sin\ x \) while \sin x gives \( \sin x \). This also works for \ln x.