Project 4: Applications of Differentiation
Instructions
Use Winplot and Google Docs to create a document with three problems on it. You may be able to locate similar problems in the book, but these problems should be your original creations.
Problem 1 - Identifying Functions
Use Winplot to create a graph that has a function and its first and second derivative graphed all on the same coordinate system. Use some scheme (color or thickness) to identify the different curves. Ask the user to identify which function is g(x), which is g'(x), and which is g''(x).
Repeat this so that you have 4 graphs all together. Mix up the graphs so there is a good selection of function types. Do not use the same color scheme for each graph.
Provide an answer key at the end of the project.
Example question 1
Identify which function is the graph of y=g(x), y=g'(x), and y=g''(x).
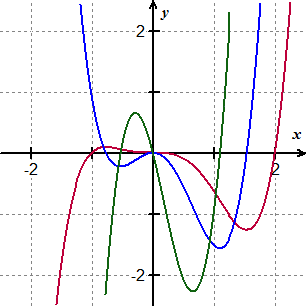
Key for question 1
The red curve is g, the blue curve is g', and the green curve is g''.
Problem 2 - Sketching Curves
You need to do this portion on paper and pencil. Either scan the document (or take a picture with your cell phone) and then upload it into the Google document. Do not shrink the size; make sure it's big enough to read everything.
Find the digit sum of the birthdates (month and day only) of the people in your group to decide which function you will use. Example: If birthdays are 1/25 and 3/18, then 1+2+5+3+1+8 = 20, then 2+0 = 2, so the digit sum is 2. You would use function #2.
Take the function determined using the digit sum method and go through the 8 step process in the textbook in section 4.4.Sketch the graph by hand on paper.
After you have done all the work by hand, use Winplot to make the graph. Be sure to change the settings on the graph so that the important features of the graph are shown.
Functions
- \( f(x) = \frac{9x}{x^2+16} \)
- \( f(x) = \frac{4x^2}{x^3+4} \)
- \( f(x) = \frac{3e^{-0.8x}}{x^2+1} \)
- \( f(x) = x^{5/3}-2x^{4/3} \)
- \( f(x) = \frac{\sin x}{2+\cos x} \)
- \( f(x) = \ln (x^2 - 4x + 5) \)
- \( f(x) = \frac{x^2-4}{x-5} \)
- \( f(x) = e^{-0.5x^2} \)
- \( f(x) = x+2\sin x \)
Maxima
Note that some of the zeros may be difficult to find by hand; you can use Maxima and its solve() or find_root() commands to assist. After typing the command, you either press shift-enter or the enter on the numeric keypad to execute the command.
Problem 3 - Newton's Method
Create a function with an x-intercept and then apply Newton's method to find that x-intercept. Continue to iterate until you get the same x-value twice in a row.
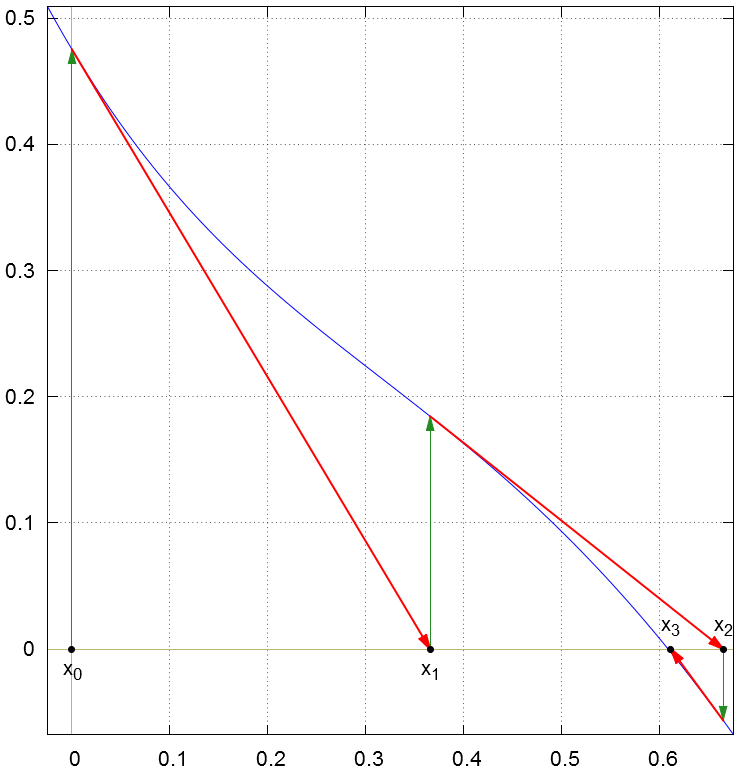
Create a graph that will illustrate Newton's method for that problem with for at least two iterations.
Example Problem 2
The function \(f(x) = (x-1)(x-3)(1-0.5e^{0.3-x^2})-0.5\) has a zero between \(x=-1\) and \(x=2\). Use Newton's Method to find it.
We'll start off with an initial guess of \(x_0 = 0\).
| \(n\) |
\(x_n\) |
\(y_n\) |
\(y_n'\) |
| 0 |
0 |
0.475211789 |
-1.300282385 |
| 1 |
0.365468143 |
0.184488271 |
-0.61695879 |
| 2 |
0.664496659 |
-0.056502485 |
-1.059827831 |
| 3 |
0.611183769 |
-0.002665516 |
-0.959869638 |
| 4 |
0.608406813 |
-7.18906E-06 |
-0.954693235 |
| 5 |
0.608399283 |
-5.3E-11 |
-0.954679209 |
| 6 |
0.608399282 |
0 |
-0.954679209 |
| 7 |
0.608399282 |
|
|
The solution is x = 0.608399282.
Additional Notes
- Add your names at the top of the document under the title.
- Include instructions with each of the problems; don’t just create a graph or describe the graph.
- To submit the assignment, click the Share button in Google Docs and change it so that anyone with the link can view the results. Then copy the share link and email it to the instructor at james@richland.edu with an appropriate subject and the names of the people in the group. Only one person per group needs to submit the project.
Winplot Tips
File Menu
- When appropriate, use Image size to create a square document. The measurements are in centimeters. While 16.5 cm will make it fill the entire page horizontally, it will also take a lot of space vertically. You may want something smaller like 11.7 or 8.1, which will allow two side-by-side images.
- Use Bitmap to clipboard to capture the image so you can paste it into Google Docs. The regular copy to clipboard doesn’t work.
- Be sure to Save your graphic so that you can re-edit later if you need to do so.
Equa Menu
- Use implicit to graph an implicit equation. Sometimes, implicit graphs have a problem displaying if you change the zoom or arrow around to change the viewing. A workaround is to edit the graph in the inventory and then change the color.
- The inventory has a derive button that will graph the derivative of the selected function. The graph button will show or hide a graph, so a good way to make matching graphs is to sketch the function and derivative to make sure both are going to fit reasonably well on in the viewing window and then show one while hiding the other when you copy and paste the graph.
View Menu
- Use Grid to control the visibility of the grid, axes, tick marks, and labels. I recommend using a rectangular grid with dotted lines in all four quadrants. Check the scale box to show the numeric labels on the axes.
- Use View to control the domain and range of the image.
Btns Menu
- Use Text to add labels to the graph. Use the right mouse button to add or edit text and the left mouse button to drag it and change its position.
Google Docs Tips
Google Docs
- Increase the font size on your document. The equations are the size of your normal font, but that may be too small to see the mathematical expressions while editing them. You can change the font size and then update the Normal text style to match. Alternatively, you can highlight the entire document and change the font size, but this may not apply to text added later.
- Click the Share button at the top right and change who has access so that anyone with the link can view the document. Then you can just submit the link.
Equations
- Use Insert > Equation to insert an equation
- Create the structure before you use it. For example, click on the fraction template before typing the numerator.
- There are some keyboard shortcuts, most notably the ^ and _ give you superscripts and subscripts.
- Matrices are not supported. That might not sound like a big deal, but the trick to displaying piecewise functions is to create a matrix to use as placeholders. In fact, multi-line equations are not supported either. Basically, you don’t want to use Google Docs for serious mathematical content, but it will allow for collaboration.
- To get mathematical functions to display properly in an equation, precede them with a backslash. For example: sin x gives \( sin\ x \) while \sin x gives \( \sin x \). This also works for \ln x.
Maxima
find_root(function, variable, lower bound, upper bound);
find_root(x^3-3*x+1,x,0,1);
will give you 0.34729635533386
The find_root() command requires a left bound and a right bound and an x-intercept in-between them. If there are multiple x-intercepts between the left and right bounds, then the results are unpredictable.
solve(equations, variables);
The variable may be omitted if it is obvious what you want. It says equations, but you can leave off the = 0.
solve(x^3-3*x+1);
will give you
- \( x={\left( \frac{\sqrt{3}\,i}{2}-\frac{1}{2}\right) }^{\frac{2}{3}}+\left( -\frac{\sqrt{3}\,i}{2}-\frac{1}{2}\right) \,{\left( \frac{\sqrt{3}\,i}{2}-\frac{1}{2}\right) }^{\frac{1}{3}}\)
- \( x={\left( \frac{\sqrt{3}\,i}{2}-\frac{1}{2}\right) }^{\frac{4}{3}}+\frac{-\frac{\sqrt{3}\,i}{2}-\frac{1}{2}}{{\left( \frac{\sqrt{3}\,i}{2}-\frac{1}{2}\right) }^{\frac{1}{3}}}\)
- \( x={\left( \frac{\sqrt{3}\,i}{2}-\frac{1}{2}\right) }^{\frac{1}{3}}+\frac{1}{{\left( \frac{\sqrt{3}\,i}{2}-\frac{1}{2}\right) }^{\frac{1}{3}}}\)
None of the results from solve are useful, but solve() is usually better when it works as it will give you all of the solutions it can find (except for ones involving periodic functions like the trigonometric functions).
You can also solve a system of equations with the solve() command, but that's not useful for this project.


