Calculating the Standard Deviation

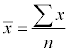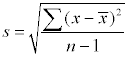The standard deviation is a measurement of dispersion that can be interpreted as the average deviation or spread from the mean.

It is calculated using the formula where the mean .

The Standard Deviation can be found using these steps.
You can see the formulas if you wish.

1. Find the mean of all the values by adding them up and dividing by the number of values.
2. Then find the deviation (difference) from the mean by subtracting the mean from each value.
3. Square the deviation from the mean for each value.
4. Total the square of the deviations from the mean.
5. Divide by the degrees of freedom (one less than the sample size)
6. Take the square root of the entire quantity.

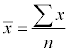
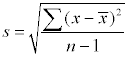
Let's consider the name JAMES.

Letter
J A M E S	10   1   13   5   19	0.400   -8.600   3.400   -4.600   9.400	0.160   73.960   11.560   21.160   88.360
Total	48		195.200

The variation

Variation: The sum of the squares of the deviations from the mean.

is the result after step 4. The variation does not involve the sample size, so we don't know if it took five numbers or fifty numbers to achieve that variation.

The variance

Variance: The average squared deviation from the mean.

is what we get when we divide the variation by the degrees of freedom. The variance doesn't have the same units as the original data, its units are squared.

The standard deviation

Standard Deviation : The average deviation from the mean.

is found by taking the square root of the variance. This returns us to the original units of the data and is the final measure of dispersion that we'll use.