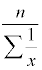Measures of Center

Common Measures of Center

Mean

The mean is the most common measure of center. It is what most people think of when they hear the word "average". However, the mean is affected by extreme values so it may not be the best measure of center to use in a skewed distribution.

Procedure for finding

1. Add all the data values together
2. Divide by the sample size

Properties

• The mean always exists
• The mean does not have to be one of the data values
• The mean uses all the data values
• The mean is affected by extreme values

Formula

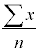
Median

The median is the value in the center of the data. Half of the values are less than the median and half of the values are more than the median. It is probably the best measure of center to use in a skewed distribution.

Procedure for finding

1. Rank the data so that it is in order from lowest to highest
2. Find the number in the middle.
   • Assuming that n is the sample size, then the depth (position) of the median is found by taking 0.5n and either rounding up (if a decimal) or adding 0.5 (if a whole number).
   • Once the depth of the median is found, the median is the value in that position. If the depth is not a whole number, then average the two adjacent values (if the depth=19.5, then average the 19th and 20th numbers).

Properties

• The median always exists.
• The median does not have to be one of the data values.
• The median does not use all of the data values, only the one(s) in the middle.
• The median is resistant to change, it is not affected by extreme values.

Midrange

The midrange is the midpoint between the lowest and highest values.

Procedure for finding

1. Add the lowest and highest values together
2. Divide by 2

Properties

• The midrange always exists
• The midrange does not have to be one of the values
• The midrange does not use all of the values, only the lowest and highest
• The midrange is greatly affected by extreme values since it uses only the extreme values.

Formula

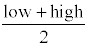
Mode

The mode is the most frequent value. If no value appears more than any other, then there is no mode. If two or more values appear more than the others, then the data is bimodal or multimodal.

Procedure for finding

1. Rank the data in order from lowest to highest. This is not necessary, but it makes it easier to count how many times a certain value appears when they are in order.
2. Find the frequency of each value.
3. The most frequent value is the mode.

Properties

• The mode may or may not exist. If it does exist, there may be one or several modes.
• The mode has to be one of the data values.
• The mode does not use all the data values.
• The is probably not affected by extreme values since it's unlikely the extreme values are not the most common.

Less Common Measures of Center

Trimmed Mean

The trimmed mean is the mean after the lowest 10% of the values and the highest 10% of the values have been removed. The trimmed mean has the benefit over the regular mean that the extreme values have been cast out and so the trimmed mean is more resistant to change than the mean.

Procedure for finding

1. Rank the data from lowest to highest.
2. Remove the smallest 10% and the largest 10% of the values from the data.
3. Add the remaining values together.
4. Divide the total by the number of remaining values.

Quadratic Mean

The quadratic mean is used in some physical applications such as power distribution systems. It is also called the Root Mean Square (R.M.S.).

Procedure for finding

1. Square each value
2. Total the squares of each value
3. Divide the total by the number of values
4. Take the square root

Formula

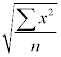
Geometric Mean

The geometric mean only exists when all of the data values are positive. It is often used when finding the average of rates of change, rates of growth, or ratios.

Procedure for finding

1. Multiply all of the data values together
2. Take the root of the product where the index is equal to the sample size. In other words, if there are 8 numbers, take the 8th root.

Formula

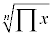
Harmonic Mean

The harmonic mean only exists when all of the values are positive. It is often used when the data consists of rates of change, such as speeds.

Procedure for finding

1. Take the reciprocal of each data value
2. Find the sum of all the reciprocals
3. Divide the sample size by the total of the reciprocals

Formula