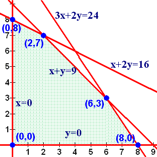
The corner points are the vertices of the feasible region. Once you have the graph of the system of linear inequalities, then you can look at the graph and easily tell where the corner points are. The corner points are the vertices of the feasible region. Once you have the graph of the system of linear inequalities, then you can look at the graph and easily tell where the corner points are.
You may need to solve a system of linear equations to find some of the coordinates of the points in the middle. For example, the solution to the intersection of thelines x + 2y = 16 and x + y = 9 is the point (2,7). This point can be found by graphing, substitution, elimination, Gaussian reduction, matrix inverses, or Cramer's rule.
For this system, the corner points are (0,0), (0,8), (2,7), (6,3), and (8,0).
Notice that each corner point is the intersection of two lines, but not every intersection of two lines is a corner point. For example, the point (6,3) is the intersection of 3x + 2y = 24 and x + y = 9, but the intersection of 3x + 2y = 24 and x + 2y = 16 is outside the feasible region, so it is not a corner point.
We're finally at the place where we're going to look at the objective function, P = 40x + 30y. Everything we've done so far has involved only the constraints or inequalities. The easiest way to do this is to make a table.
| x | y | P = 40x + 30y |
|---|---|---|
| 0 | 0 | 0 + 0 = 0 |
| 0 | 8 | 0 + 240 = 240 |
| 2 | 7 | 80+210 = 290 |
| 6 | 3 | 240 + 90 = 330 |
| 8 | 0 | 320 + 0 = 320 |
Since the objective was to maximize P and the largest value of P occurs when x = 6 and y = 3, we can give the answer to the linear programming problem.
The maximum value of P is 330 when x = 6 and y = 3.
If the objective had been to maximize P, then we could say the minimum value of P is 0 when x = 0 and y = 0.
Let's say that you had the same feasible region, but different objective functions.
The easiest way to accomplish this is to just extend the table with additional columns for each of the other objective functions.
| x | y | 40x+30y | 20x+30y | 10x+30y | 50x+30y | 30x+30y |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 8 | 240 | 240 | 240 | 240 | 240 |
| 2 | 7 | 290 | 250 | 230 | 310 | 270 |
| 6 | 3 | 330 | 210 | 150 | 390 | 270 |
| 8 | 0 | 320 | 160 | 80 | 400 | 240 |
In each case, the maximum value has been bolded so you can see where it is.
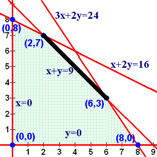Notice that last one gives us a slight problem. The maximum value of 270 occurs not only when x = 2 and y = 7 but also when x = 6 and y = 3. In fact, it also occurs when x = 3 and y = 6, when x = 4 and y = 5, when x = 5 and y = 4, when x = 4.6 and y = 4.4, and any other point on the line segment between (2,7) and (6,3).
This is the case where the fundamental theorem of linear programming mentioned that the solution was the boundary between two corner points. Every point between (2,7) and (6,3) is on the line x + y = 9.
But not every point on the line x + y = 9 is a solution. For example, x = 1 and y = 8 is not even in the feasible region. So, we need to restrict our domain to just the portion of the line segment we need.
So now we can answer that last problem.
The maximize value of P = 30x + 30y is 270 when x + y = 9 and 2 ≤ x ≤ 6.
Alternatively, you could use parametric form and say the maximum value of P is 270 when x = 2 + 4t, y = 7- 4t, 0 ≤ t ≤ 1. Most people will find the first form easier.