Central Limit Theorem

---

Sampling Distribution of the Sample Means

Instead of working with individual scores, statisticians often work with means. What happens is that several samples are taken, the mean is computed for each sample, and then the means are used as the data, rather than individual scores being used. The sample is a sampling distribution of the sample means.

Examples

Example 1: Sampling Distribution of Values (x)

Consider the case where a single, fair die is rolled.

Here are the values that are possible and their probabilities.

Value	1	2	3	4	5	6
Probability	1/6	1/6	1/6	1/6	1/6	1/6

Here are the mean, variance, and standard deviation of this probability distribution.

Mean, mu = sum [ x * p(x) ] = 3.5
Variance, sigma^2 = sum [ x^2 * p(x) ] - mu^2 = 35/12
Standard deviation, sigma = sqrt ( variance ) = sqrt ( 35/12 )

Example 2: Sampling Distribution of Sample Means (x-bar)

Consider the case where two fair dice are rolled instead of one.

Here are the sums that are possible and their probabilities.

Sum	2	3	4	5	6	7	8	9	10	11	12
Prob	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

But, we're not interested in the sum of the dice, we're interested in the sample mean. We find the sample mean by dividing the sum by the sample size.

Mean	1.0	1.5	2.0	2.5	3.0	3.5	4.0	4.5	5.0	5.5	6.0
Prob	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

Computing the mean, variance, and standard deviation, we get ...

Mean, mu = sum [ x * p(x) ] = 3.5
Variance, sigma^2 = sum [ x^2 * p(x) ] - mu^2 = 35/24
Standard deviation, sigma = sqrt ( variance ) = sqrt ( 35/24 )

Properties of the Sampling Distribution of the Sample Means

When all of the possible sample means are computed, then the following properties are true:

• The mean of the sample means will be the mean of the population
• The variance of the sample means will be the variance of the population divided by the sample size.
• The standard deviation of the sample means (known as the standard error of the mean) will be smaller than the population mean and will be equal to the standard deviation of the population divided by the square root of the sample size.
• If the population has a normal distribution, then the sample means will have a normal distribution.
• If the population is not normally distributed, but the sample size is sufficiently large, then the sample means will have an approximately normal distribution. Some books define sufficiently large as at least 30 and others as at least 31.

The formula for a z-score when working with the sample means is: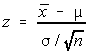

Finite Population Correction Factor

If the sample size is more than 5% of the population size and the sampling is done without replacement, then a correction needs to be made to the standard error of the means.

In the following, N is the population size and n is the sample size. The adjustment is to multiply the standard error by the square root of the quotient of the difference between the population and sample sizes and one less than the population size.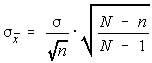

For the most part, we will be ignoring this in class.