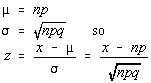
You are estimating the population proportion, p.
All estimation done here is based on the fact that the normal can be used to approximate the binomial distribution when np and nq are both at least 5. Thus, the p that were talking about is the probability of success on a single trial from the binomial experiments.
Recall: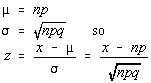
The best point estimate for p is p hat, the sample proportion: 
If the formula for z is divided by n in both the numerator and the denominator, then the formula
for z becomes: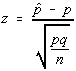 
Solving this for p to come up with a confidence interval, gives the maximum error of the estimate
as: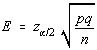 
.
This is not, however, the formula that we will use. The problem with estimation is that you don't know the value of the parameter (in this case p), so you can't use it to estimate itself - if you knew it, then there would be no problem to work out. So we will replace the parameter by the statistic in the formula for the maximum error of the estimate.
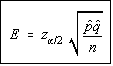The maximum error of the estimate is given by the formula for E shown.
The Z here is the z-score obtained from the normal table, or the bottom of
the t-table as explained in the introduction to estimation. The z-score is a
factor of the level of confidence, so you may get in the habit of writing it
next to the level of confidence.
When you're computing E, I suggest that you find the sample proportion, p hat, and save it to P on the calculator. This way, you can find q as (1-p). Do NOT round the value for p hat and use the rounded value in the calculations. This will lead to error. Once you have computed E, I suggest you save it to the memory on your calculator. On the TI-82, a good choice would be the letter E. The reason for this is that the limits for the confidence interval are now found by subtracting and adding the maximum error of the estimate from/to the sample proportion.
