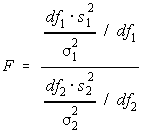F-Test

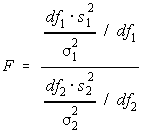The F-distribution is formed by the ratio of two independent chi-square variables divided by their respective degrees of freedom.

Since F is formed by chi-square, many of the chi-square properties carry over to the F distribution.

• The F-values are all non-negative
• The distribution is non-symmetric
• The mean is approximately 1
• There are two independent degrees of freedom, one for the numerator, and one for the denominator.
• There are many different F distributions, one for each pair of degrees of freedom.

F-Test

The F-test is designed to test if two population variances are equal. It does this by comparing the ratio of two variances. So, if the variances are equal, the ratio of the variances will be 1.

All hypothesis testing is done under the assumption the null hypothesis is true

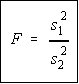If the null hypothesis is true, then the F test-statistic given above can be simplified (dramatically). This ratio of sample variances will be test statistic used. If the null hypothesis is false, then we will reject the null hypothesis that the ratio was equal to 1 and our assumption that they were equal.

The F test statistic is simply the ratio of two sample variances.

There are several different F-tables. Each one has a different level of significance. So, find the correct level of significance first, and then look up the numerator degrees of freedom and the denominator degrees of freedom to find the critical value.

You will notice that all of the tables only give level of significance for right tail tests. Because the F distribution is not symmetric, and there are no negative values, you may not simply take the opposite of the right critical value to find the left critical value. The way to find a left critical value is to reverse the degrees of freedom, look up the right critical value, and then take the reciprocal of this value. For example, the critical value with 0.05 on the left with 12 numerator and 15 denominator degrees of freedom is found of taking the reciprocal of the critical value with 0.05 on the right with 15 numerator and 12 denominator degrees of freedom.

Avoiding Left Critical Values

Since the left critical values are a pain to calculate, they are often avoided altogether. This is the procedure followed in the textbook. You can force the F test into a right tail test by placing the sample with the large variance in the numerator and the smaller variance in the denominator. It does not matter which sample has the larger sample size, only which sample has the larger variance.

The numerator degrees of freedom will be the degrees of freedom for whichever sample has the larger variance (since it is in the numerator) and the denominator degrees of freedom will be the degrees of freedom for whichever sample has the smaller variance (since it is in the denominator).

If a two-tail test is being conducted, you still have to divide alpha by 2, but you only look up and compare the right critical value.

Assumptions / Notes

• The larger variance should always be placed in the numerator
• The test statistic is F = s₁² / s₂² where s₁² > s₂²
• Divide alpha by 2 for a two tail test and then find the right critical value
• If standard deviations are given instead of variances, they must be squared
• When the degrees of freedom aren't given in the table, go with the value with the larger critical value (this happens to be the smaller degrees of freedom). This is so that you are less likely to reject in error (type I error)
• The populations from which the samples were obtained must be normal.
• The samples must be independent