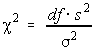Single Population Variance

The variable 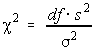has a chi-square distribution if the population variance has a normal distribution. The degrees of freedom are n-1. We can use this to test the population variance under certain conditions

Conditions for testing

• The population has a normal distribution
• The data is from a random sample
• The observations must be independent of each other
• The test statistic has a chi-square distribution with n-1 degrees of freedom and is given by:

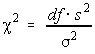
Testing is done in the same manner as before. Remember, all hypothesis testing is done under the assumption the null hypothesis is true.

Confidence Intervals

If you solve the test statistic formula for the population variance, you get: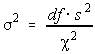

1. Find the two critical values (alpha/2 and 1-alpha/2)
2. Compute the value for the population variance given above.
3. Place the population variance between the two values calculated in step 2 (put the smaller one first).

Note, the left-hand endpoint of the confidence interval comes when the right critical value is used and the right-hand endpoint of the confidence interval comes when the left critical value is used. This is because the critical values are in the denominator and so dividing by the larger critical value (right tail) gives the smaller endpoint.