( x - h )2 = 4 p ( y - k )The only difference between this section and the last section is that in this section, the conics have gone through a rigid transformation and been shifted vertically or horizontally.
By replacing every x with an x-h and every y with a y-k, what used to be at the origin is now at the point (h,k). All movement is then relative to that point.
Eccentricity, is the ratio of the distance to the focus divided by the distance to the vertex. That is, e=c/a.
Each conic section has an eccentricity.
| Conic | Eccentricity |
|---|---|
| Circle | e = 0 |
| Ellipse | 0 < e < 1 |
| Parabola | e = 1 |
| Hyperbola | e > 1 |
Eccentricity is often used in astronomy to describe the path of the planets, moons, or comets which orbit another object.
The vertex of the parabola used to be at the origin. The vertex will now be at the point (h,k).
( x - h )2 = 4 p ( y - k )
The vertex is at (h,k).
Since the axis of symmetry is vertical, the foci and directrix have different y coordinates than the vertex.
Since p is the directed distance from the vertex to the focus, the focus will be at (h,k+p)
Since the directrix is p units the other side of the vertex, the equation of the directrix will be y=k-p
The parabola will open up if p is positive and down if p is negative.
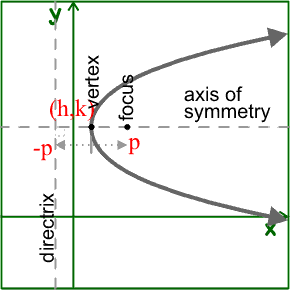( y - k )2 = 4 p ( x - h )
The vertex is at (h,k).
Since the axis of symmetry is horizontal, the foci and directrix have different x coordinates than the vertex.
Since p is the directed distance from the vertex to the focus, the focus will be at (h+p,k)
Since the directrix is p units the other side of the vertex, the equation of the directrix will be x=h-p
The parabola will open right if p is positive and left if p is negative.
( x - h )2 + ( y - k )2 = r2
The center of the circle used to be at the origin. The center will now be at the point (h,k).
The center of the ellipse used to be at the origin. The center will now be at the point (h,k).
Recall that for an ellipse, the distance from the center to the vertices is a, the distance from the center to the foci is c, and the distance from the center to the endpoints of the minor axis is b. The longest of these lengths is the distance to the vertices, so the Pythagorean identity for an ellipse is a2 = b2 + c2.
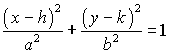
Since the major axis is horizontal, the foci and vertices will have different x coordinates than the center.
Since a is the distance from the center to the vertices, the vertices will be at (h+a,k) and (h-a,k)
Since c is the distance from the center to the foci, the foci will be at (h+c,k) and (h-c,k).
Since b is the distance from the center to the endpoints of the minor axis, and the minor axis is vertical, the endpoints of the minor axis will be at (h,k+b) and (h,k-b).
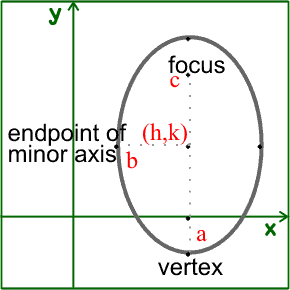
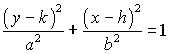
Since the major axis is vertical, the foci and vertices will have different y coordinates than the center.
Since a is the distance from the center to the vertices, the vertices will be at (h,k+a) and (h,k-a)
Since c is the distance from the center to the foci, the foci will be at (h,k+c) and (h,k-c).
Since b is the distance from the center to the endpoints of the minor axis, and the minor axis is horizontal, the endpoints of the minor axis will be at (h+b,k) and (h-b,k).
The center of the hyperbola used to be at the origin. The center will now be at the point (h,k).
Recall that for a hyperbola, the distance from the center to the vertices is a, the distance from the center to the foci is c, and the distance from the center to the endpoints of the conjugate axis is b. The longest of these lengths is the distance to the foci, so the Pythagorean identity for a hyperbola is a2 + b2 = c2.
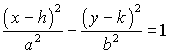
The center is at (h,k)
Since the transverse axis is horizontal, the foci and vertices will have different x coordinates than the center.
Since a is the distance from the center to the vertices, the vertices will be at (h+a,k) and (h-a,k)
Since c is the distance from the center to the foci, the foci will be at (h+c,k) and (h-c,k).
Since b is the distance from the center to the endpoints of the conjugate axis, and the conjugate axis is vertical, the endpoints of the conjugate axis will be at (h,k+b) and (h,k-b).
Since the change in y is b and the change in x is a, the slope of they asymptotes will be ±b/a. The equations of the asymptotes will be (y-k) = ± b/a (x-h).
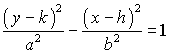
The center is at (h,k)
Since the transverse axis is vertical, the foci and vertices will have different y coordinates than the center.
Since a is the distance from the center to the vertices, the vertices will be at (h,k+a) and (h,k-a)
Since c is the distance from the center to the foci, the foci will be at (h,k+c) and (h,k-c).
Since b is the distance from the center to the endpoints of the conjugate axis, and the conjugate axis is horizontal, the endpoints of the conjugate axis will be at (h+b,k) and (h-b,k).
Since the change in y is a and the change in x is b, the slope of they asymptotes will be ±a/b. The equations of the asymptotes will be (y-k) = ± a/b (x-h).