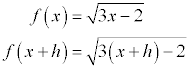
The sum, difference, product, or quotient of functions can be found easily.
The domain of each of these combinations is the intersection of the domain of f and the domain of g. In other words, both functions must be defined at a point for the combination to be defined. One additional requirement for the division of functions is that the denominator can't be zero, but we knew that because it's part of the implied domain.
Basically what the above says is that to evaluate a combination of functions, you may combine the functions and then evaluate or you may evaluate each function and then combine.
In the following examples, let f(x) = 5x+2 and g(x) = x2-1. We will then evaluate each combination at the point x=4. f(4)=5(4)+2=22 and g(4)=42-1=15
| Expression | Combine, then evaluate | Evaluate, then combine | |||
|---|---|---|---|---|---|
| (f+g)(x) | (5x+2) + (x2-1) =x2+5x+1 |
(f+g)(4) | 42+5(4)+1 =16+20+1 =37 |
f(4)+g(4) | 22+15 =37 |
| (f-g)(x) | (5x+2) - (x2-1) =-x2+5x+3 |
(f-g)(4) | -42+5(4)+3 =-16+20+3 =7 |
f(4)-g(4) | 22-15 =7 |
| (f·g)(x) | (5x+2)*(x2-1) =5x3+2x2-5x-2 |
(f·g)(4) | 5(43)+2(42)-5(4)-2 =5(64)+2(16)-20-2 =330 |
f(4)·g(4) | 22(15) =330 |
| (f/g)(4) | (5x+2)/(x2-1) | (f/g)(4) | [5(4)+2]/[42-1] =22/15 |
f(4)/g(4) | 22/15 |
As you can see from the examples, it doesn't matter if you combine and then evaluate or if you evaluate and then combine.
In each of the above problems, the domain is all real numbers with the exception of the division. The domain in the division combination is all real numbers except for 1 and -1.
While the arithmetic combinations of functions are straightforward and fairly easy, there is another type of combination called a composition.
A composition of functions is the applying of one function to another function. The symbol of composition of functions is a small circle between the function names. I can't do that symbol in text mode on the web, so I'll use a lower case oh "o" to represent composition of functions.
These are read "f composed with g of x" and "g composed with f of x" respectively.
The function on the outside is always written first with the functions that follow being on the inside. The order is important. Composition of functions is not commutative.
That doesn't sound that bad. Let's look at a few examples.
f(x)=5x+2 and g(x)=x2-1
f(x) = sqrt(x) and g(x) = 4x2
This example probably needs some explanation. From the prerequisite chapter, the square root of (x2) is the absolute value of x. The square of (the square root of x) is x, but this assumes that x is not negative because you couldn't find the square root of x in the first place if it was. This is a case where the implied domain (because of the square root) is no longer implied (because the square root is gone), so you have to explicitly state it (I told you it all fit together).
f(x) = sqrt(x-4) and g(x) = 1 - x2
If the last example needed some explanation, then this one definitely needs some, too. Let's take the easier one (gof)(x) first. There was an implied domain of x ≥ 4 because of the square root, but after squaring it, it was no longer implied, so it needed to be stated explicitly.
Okay, now for the harder one (fog)(x). I'll give the simple explanation here and the more complete one later. After simplifying, you got the square root of (-x2 - 3). -x2-3 is always negative, no matter what real number x is, and you can't take the square root of a negative number, so it is always undefined (for the set of reals).
When you find a composition of a functions, it is no longer x that is being plugged into the outer function, it is the inner function evaluated at x. So there are two domains that we have to be concerned about. If we consider (fog)(x), we see that g is evaluated at x, so x has to be in the domain of g. We also see that f is evaluated at g(x), so g(x) has to be in the domain of f.
But, it's not as bad as it looks, either. Let's consider that last example again.
| Function | Domain | Range |
|---|---|---|
| f(x) = sqrt(x-4) | x ≥ 4 | y ≥ 0 |
| g(x) = 1-x2 | all reals | y ≤ 1 |
When you find (fog)(x), there are two things that must be satisfied:
When you combine the two domains to see what they have in common, you find the intersection of everything and nothing is nothing (the empty set), so the function is defined nowhere and undefined everywhere.
When you find (gof)(x), there are two things that must be satisfied:
When you combine the two domains to see what they have in common, you find the intersection to be x ≥ 4, so that is the where the composition is defined.
Decomposition of functions is the reverse of composition of functions. Instead of combining two functions to get a new function, you're breaking apart a combined function into its separate components. There is often more than one way to decompose a function, so your answers may vary from the books.
Basically, you want to look at the function and look for an "outside function" and an "inside function". Another thing to look for is repeated patterns and make that the inside function. The outside function is summarized as "the big picture" and the inside function is "what you are doing the big picture to".
Write each function h as the composition of two functions f and g such that h(x)=(fog)(x)
| h(x) | Outside f(x) |
Inside g(x) |
Notes |
|---|---|---|---|
| (1-x)3 | x3 | 1-x | The big thing going on is cubing something, so the outside function is a cubing function. 1-x is what you're cubing, so it's the inside function. |
| sqrt(9-x) | sqrt(x) | 9-x | The big thing going on is taking the square root (outside), 9-x is what you're taking the square root of (inside) |
| 4/(5x2+2)2 | 4/x2 | 5x2+2 | Looks like 4 over something squared |
| 4/x | (5x2+2)2 | An alternative, but correct answer. | |
| (x+2)2+2(x+2)+1 | x2+2x+1 | x+2 | x+2 is repeated, so that's a good choice for the inside function. Replace every occurrence of the pattern by x for the outside function |
Difference quotients are what they say they are. They involve a difference and a quotient. A difference quotient is really the slope of a secant line between two points on a curve.
The formula for the difference quotient is: [ f(x+h) - f(x) ] / h
If you go on to calculus, you will be introduced to the concept of limits (Calculus is Algebra with limits) and find as the two points on the curve get closer together, the secant line turns into a tangent line, and the slope of the secant line becomes the slope of the tangent line which is called the derivative of the function and there are a whole lot of shortcuts for finding derivatives. However, you're still in College Algebra and don't know about limits until chapter 3 when we talk about asymptotes, so you'll have to find the difference quotients by hand. The difference quotient is very important in Calculus, so if you are going on, make sure you get this!
For polynomial functions, finding the difference quotient isn't that difficult. Where you're going to run into trouble is with radical and rational functions.
f(x) = 5x2 - 2
f(x+h) = 5(x+h)2 - 2 = 5( x2 + 2xh + h2 ) - 2 = 5x2 + 10xh + 5h2 - 2
f(x+h) - f(x) = 5( x2 + 2xh + h2 ) - 2 = 5x2 + 10xh + 5h2 - 2 - ( 5x2 - 2 )
f(x+h) - f(x) = 5x2 + 10xh + 5h2 - 2 - 5x2 + 2 = 10xh + 5h2
f(x+h) - f(x) = h ( 10x + 5h )
[f(x+h) - f(x)] / h = h ( 10x + 5h ) / h = 10x + 5h
The trick with rational functions is to get a common denominator and then simplify.
f(x) = 3 / x
f(x+h) = 3 / (x+h)
f(x+h) - f(x) = 3 / (x+h) - 3 / x
f(x+h) - f(x) = 3 x / [ x(x+h)] - 3(x+h) / [x(x+h)]
f(x+h) - f(x) = ( 3x - 3x - 3h ) / [ x(x+h) ]
f(x+h) - f(x) = -3h / [x(x+h)]
[f(x+h) - f(x)] / h = -3h / [x(x+h)] / h = -3 / [ x(x+h) ]
The trick with a radical function is to rationalize the numerator by multiplying by the conjugate of the numerator.
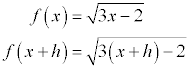
![]()
![f(x+h)-f(x)=[sqrt(3(x+h)-2)-sqrt(3x-2)]*[[sqrt(3(x+h)-2)+sqrt(3x-2)]/[sqrt(3(x+h)-2)+sqrt(3x-2)]](raddiff3.gif)
![f(x+h)-f(x)=[(3(x+h)-2)-(3x-2)]/[sqrt(3(x+h)-2)+sqrt(3x-2)]](raddiff4.gif)
![f(x+h)-f(x)=[3x+3h-2-3x+2]/[sqrt(3(x+h)-2)+sqrt(3x-2)]](raddiff5.gif)
![f(x+h)-f(x)=[3h]/[sqrt(3(x+h)-2)+sqrt(3x-2)]](raddiff6.gif)
![[f(x+h)-f(x)]/h=[3h]/[sqrt(3(x+h)-2)+sqrt(3x-2)]*(1/h)](raddiff7.gif)
![[f(x+h)-f(x)]/h=3/[sqrt(3(x+h)-2)+sqrt(3x-2)]](raddiff8.gif)
Don't worry that you're left with a radical in the denominator, it's okay in this instance. It's much better than having a factor of h in the denominator because in calculus, we're going to let h approach 0 and we'll want to just plug a zero in for h. When given the choice of having a radical in the denominator or division by 0, we'll pick a radical in the denominator anyday.