1.4 - Graphs of Functions
Definitions
These definitions are mathematically loose (that means a mathematician would
pull his or her hair out but a normal person might understand them).
- Graph of a function
- The graph of a function f is the set of all ordered pairs ( x, f(x) ) where x is in the
domain of f.
- Increasing Function
- A function is increasing on an open interval if the function rises (positive slope) on the
interval as you move from left to right.
- Decreasing Function
- A function is decreasing on an open interval if the function falls (negative slope) on the
interval as you move from left to right.
- Constant Function
- A function is constant on an open interval if the function remains constant (horizontal
line segment) on the interval as you move from left to right.
- Relative Minimum
- A function has a relative minimum at x=a if the function evaluated at x=a is less than at
any other point in the neighborhood surrounding x=a. A relative minimum is the
lowest point in an open interval, but not necessarily over the entire domain. Relative
minimums occur when the function is decreasing to the left of the point and increasing
to the right of the point.
- Relative Maximum
- A function has a relative maximum at x=a if the function evaluated at x=a is greater
than at any other point in the neighborhood surrounding x=a. A relative maximum is
the highest point in an open interval, but not necessarily over the entire domain.
Relative maximums occur when the function is increasing to the left of the point and
decreasing to the right of the point.
- Greatest Integer Function
- The greatest integer of a value is the largest integer less than or equal to the value.
- Symmetry about the y-axis
- A relation is symmetric about the y-axis if for every point (x,y) on the graph, the point
(-x,y) is also on the graph.
- Symmetry about the x-axis
- A relation is symmetric about the x-axis if for every point (x,y) on the graph, the point
(x,-y) is also on the graph.
- Symmetry about the origin
- A relation is symmetric about the origin if for every point (x,y) on the graph, the point
(-x,-y) is also on the graph.
- Even Function
- A function is even if for every x in the domain of the function, f(-x) = f(x)
- Odd Function
- A function is odd if for every x in the domain of the function, f(-x) = -f(x)
Vertical Line Test
A relation is a function if all vertical lines drawn through the graph of the relation intersect
in no more than one point.
The contrapositive of that is often used.
If a vertical line intersects the graph of a relation in two or more points, then the relation is
not a function.
Greatest Integer Function
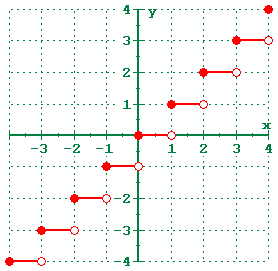The greatest integer function is often called the Integer function (or Floor in upper level
mathematics), and is abbreviated INT on the calculator. You may find the INT function on the
calculator by going into the [Math] menu, arrowing right to the NUM option, and then choosing
the INT function (it's number 5 on the TI83).
The Integer function is sometimes called the step function because of the stair step effect
obtained when graphing it. Be sure to use a decimal setting when graphing the greatest integer
function, or you will get weird results. You may also want to use Dot mode instead of Connected
mode when graphing the Integer function. You can change modes on the TI series by hitting the
[Mode] key.
Mathematically, the greatest integer function is represented using a double left bracket and
double right bracket
Symmetry - Odd / Even Functions
- Symmetry about the y-axis
- Symmetry about the y-axis means that the left side of the graph is a mirror image of the
right side of the graph. Mathematically, a relation which is symmetric about the y-axis
has the property that for every point (x,y) that is on the graph, the point (-x,y) is also on
the graph. In other words, to mirror something about the y-axis, take the opposite of all
the x-coordinates and leave the y-coordinates alone.
- Symmetry about the x-axis
- Symmetry about the x-axis means that the bottom side of the graph is a mirror image of
the top side of the graph. Mathematically, a relation which is symmetric about the x-axis has the property that for every point (x,y) that is on the graph, the point (x,-y) is
also on the graph. In other words, to mirror something about the x-axis, take the
opposite of all the y-coordinates and leave the x-coordinates alone.
- Symmetry about the origin
- Symmetry about the origin means that for every point (x,y) on the graph, the point (-x,-y) is also on the graph. Graphically, to create symmetry about the origin, take any
point, draw an imaginary line through the origin, and place a point on that line the same
distance as the original point was from the origin on the other side of the origin.
- Even Function
- A function is even if it is symmetric about the y-axis. Mathematically, since the y-coordinates (values of the function) have to be equal, and the x-coordinates are
opposite, one can write: f(-x) = f(x).
- There is a reason these functions are called even. If you have a polynomial function in
one variable, all of the exponents on the independent variable will be even. Remember
that a constant is the zero power of the variable and zero is even.
- Odd Function
- A function is odd if it is symmetric about the origin. Mathematically, since both the x-coordinate and the y-coordinates are negated, one can write: f(-x) = -f(x).
- There is a reason these functions are called odd. If you have a polynomial function in
one variable, all of the exponents on the independent variable will be odd. Remember
that a constant is the zero power of a variable and will be even, so if there is a constant
term, it is not an odd function.