4.2 - Logarithmic Functions and Their Graphs
Inverse of Exponential Functions
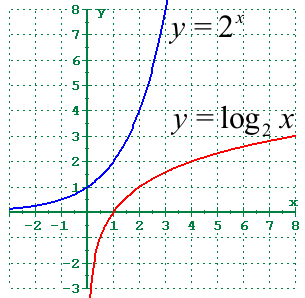 We stated in the section on exponential functions, that
exponential functions were one-to-one. One-to-one
functions had the special property that they have inverses
that are also functions. And, as many of you said in class,
and I'm so glad you remember, one-to-one functions can
be applied to both sides of an equation. They also pass a
horizontal line test.
We stated in the section on exponential functions, that
exponential functions were one-to-one. One-to-one
functions had the special property that they have inverses
that are also functions. And, as many of you said in class,
and I'm so glad you remember, one-to-one functions can
be applied to both sides of an equation. They also pass a
horizontal line test.
This section is about the inverse of the exponential
function. The inverse of an exponential function is a
logarithmic function. Remember that the inverse of a
function is obtained by switching the x and y coordinates. This reflects the
graph about the line y=x. As you can tell from the graph to the right, the
logarithmic curve is a reflection of the exponential curve.
The table below demonstrates how the x and y values of the points on the expontential
curve can be switched to find the coordinates of the points on the logarithmic
curve.
Point on
exponential curve |
Corresponding point
on logarithmic curve |
| (-3, 1/8) |
(1/8, -3) |
| (-2, 1/4) |
(1/4, -2) |
| (-1, 1/2) |
(1/2, -1) |
| (0, 1) |
(1, 0) |
| (1, 2) |
(2, 1) |
| (2, 4) |
(4, 2) |
| (3, 8) |
(8, 3) |
Comparison of Exponential and Logarithmic Functions
Let's look at some of the properties
of the two functions.
The standard form for a logarithmic function is: y = loga x
Note, if the "a" in the expression above is not a subscript (lower than
the "log"),
then you need to update your
web browser.
| |
Exponential |
Logarithmic |
| Function |
y=ax, a>0, a≠1 |
y=loga x, a>0, a≠1 |
| Domain |
all reals |
x > 0 |
| Range |
y > 0 |
all reals |
| intercept |
y = 1 |
x = 1 |
| increasing |
when a > 1 |
when a > 1 |
| decreasing |
when 0 < a < 1 |
when 0 < a < 1 |
| asymptote |
y-axis |
x-axis |
| continuous |
yes |
yes |
| smooth |
yes |
yes |
Working Definition of Logarithm
In the exponential function, the x was the exponent. The purpose of the inverse of a function is
to tell you what x value was used when you already know the y value. So, the purpose of the
logarithm is to tell you the exponent.
Thus, our simple definition of a logarithm is that it is an exponent.
Another way of looking at the expression "loga x" is "to what power (exponent) must a be raised
to get x?"
Equivalent Forms
The logarithmic form of the equation y=loga x is equivalent to the exponential form x=ay.
To rewrite one form in the other, keep the base the same, and switch sides with the other two
values.
Properties of Logarithms
- loga 1 = 0 because a0 =
1
- No matter what the base is, as long as it is legal, the log of 1 is always 0.
That's because
logarithmic curves always pass through (1,0)
- loga a = 1 because a1 = a
- Any value raised to the first power is that
same value.
- loga ax = x
- The log base a of x and a to the x power are inverse functions. Whenever inverse
functions are applied to each other, they inverse out, and you're left with
the
argument, in this case, x.
- loga x = loga y implies that x = y
- If two logs with the same base are equal, then
the arguments must be equal.
- loga x = logb x implies that a = b
- If two logarithms with the same argument are
equal, then the bases must be equal.
Common Logs and Natural Logs
There are two logarithm buttons on your calculator. One is marked "log" and
the other is marked
"ln". Neither one of these has the base written in. The base can be determined,
however, by looking at the inverse function, which is written above the key and
accessed by the 2nd key.
Common Logarithm (base 10)
When you see "log" written, with no base, assume the base is 10.
That is: log x = log10 x.
Some of the applications that use common logarithms are in pH (to measure acidity), decibels
(sound intensity), the Richter scale (earthquakes).
An interesting (possibly) side note about pH. "Chapter 50: Sewers" of the Village
of Forsyth Code requires forbids the discharge of waste with a pH of less than
5.5 or higher than 10.5
(section 50.07).
Common logs also serve another purpose. Every increase of 1 in a common logarithm
is the result of 10 times the argument. That is, an earthquake of 6.3 has 10
times the magnitude of a
5.3 earthquake. The decibel level of loud rock music or a chainsaw (115 decibels
= 11.5 bels) is 10 times
louder than chickens inside a building (105 decibels = 10.5 bels)
Natural Logarithms (base e)
Remember that number e, that we had from the previous section? You know, the one that was
approximately 2.718281828 (but doesn't repeat or terminate). That is the base for the natural
logarithm.
When you see "ln" written, the base is e.
That is: ln x = loge x
Exponential growth and decay models are one application that use natural logarithms. This
includes continuous compounding, radioactive decay (half-life), population growth. Typically
applications where a process is continually happening. Now, these applications were first
mentioned in the exponential section, but you will be able to solve for the other variables
involved (after section 4) using logarithms.
In higher level mathematics, the natural logarithm is the logarithm of choice. There are several
special properties of the natural logarithm function, and it's inverse function, that make life much
easier in calculus.
Since "ln x" and "ex" are inverse functions of each other, any time an "ln" and "e" appear right
next to each other, with absolutely nothing in between them (that is, when they
are composed with each other), then they inverse out, and you're left with
the argument.
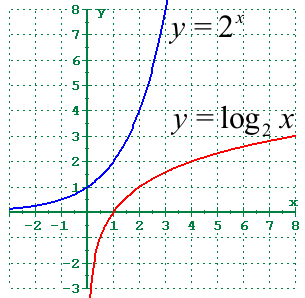 We stated in the section on exponential functions, that
exponential functions were one-to-one. One-to-one
functions had the special property that they have inverses
that are also functions. And, as many of you said in class,
and I'm so glad you remember, one-to-one functions can
be applied to both sides of an equation. They also pass a
horizontal line test.
We stated in the section on exponential functions, that
exponential functions were one-to-one. One-to-one
functions had the special property that they have inverses
that are also functions. And, as many of you said in class,
and I'm so glad you remember, one-to-one functions can
be applied to both sides of an equation. They also pass a
horizontal line test.