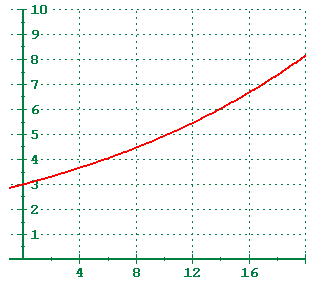
FunctionFunctiony = C ekt, k > 0
Some of the things that exponential growth is used to model include population growth, bacterial growth, and compound interest.
If you are lucky enough to be given the initial value, that is the value when x = 0, then you already know the value of the constant C. The only thing necessary to complete the model is to have one additional point on the graph. Plug in the values for x, y, and C, and solve for k.
Alternatively, almost like cheating, you can put the x-values into List 1, the y-values into List 2, and choose the ExpReg option on the TI-82 calculator.
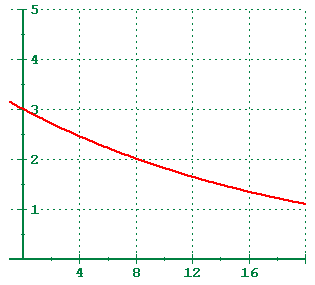Functiony = C e-kt, k > 0
Exponential decay and be used to model radioactive decay and depreciation.
Exponential decay models decrease very rapidly, and then level off to become asymptotic towards the x-axis.
Like the exponential growth model, if you know the initial value then the rest of the model is fairly easy to complete.
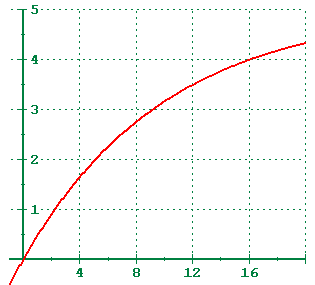Functiony = C ( 1 - e-kt ), k > 0
Exponential decay models of this form can model sales or learning curves where there is an upper limit. This is done by subtracting the exponential expression from one and multiplying by the upper limit.
Exponential decay models of this form will increase very rapidly at first, and then level off to become asymptotic to the upper limit.
Like the other exponential models, if you know upper limit, then the rest of the model is fairly easy to complete.
The calculator will not fit the increasing model involving exponential decay directly.
Functiony = a exp (-(x-c) / b)2
exp(x) is another way of writing ex
The Gaussian model is used quite a bit in Statistics to model the distribution of scores.
The Gaussian model is named after the German mathematician Carl Friedrich Gauss. This is the same Gauss who developed the Fundamental Theorem of Algebra. It is symmetric about its mean, x = c. To the right of the origin, it decreases slowly at first, then more rapidly, and then levels off and become asymptotic to the x-axis.
Like the Exponential Decay model, the Gaussian model can be turned into an increasing function by subtracting the exponential expression from one and then multiplying by the upper limit.
Functiony = a / (1 + b e-kx ), k > 0
My personal favorite, the logistics model begins with a slow growth, followed by a period of moderate growth, and then back to a period of slow growth. It has an upper limit that cannot be exceeded.
The Logistics model can be used to approximate sales and advertising (a little advertising generates a little growth in sales, more advertising generates moderate growth in sales, and finally there reaches a point of saturation where additional advertising benefits little in terms of sales) or population growth where there is not the capacity for unlimited growth (use the exponential growth model if you need that).
Functiony = a + b ln x
The logarithmic model has a period of rapid increase, followed by a period where the growth slows, but the growth continues to increase without bound. This makes the model inappropriate where there needs to be an upper bound. The main difference between this model and the exponential growth model is that the exponential growth model begins slowly and then increases very rapidly as time increases.
Several physical applications have logarithmic models. The magnitude of earthquakes, the intensity of sound, the acidity of a solution.
R = log I
The Richter scale is used to measure the intensity of an earthquake. The actual model is a little more complex, but it simplifies to the equation shown. R is the magnitude on the Richter scale of the earthquake. I is the intensity of the earthquake measured relative to a reference value. That reference value is the smallest seismic activity that can be measured, and has the value I0 = 1.
Every increase of 1 in the Richter scale means the magnitude of the earthquake is 10 times greater.
β = 10 log ( I / I0 )
The sound level, measured in decibels, is given by the formula shown. The reference value, I0 is the smallest sound intensity which can be heard by the human ear and is roughly equal to 1x10-16 watts per square centimeter.
There are 10 decibels to a bel. While bel is the actual unit, like meter, liter, or gram, we use decibel for all practical purposes. An increase of 10 decibels is equivalent to a sound that is 10 times as strong in intensity. An increase of 20 decibels is equivalent to a sound intensity that is 100 times greater.
pH = - log [ H+ ]
pH is a measure of the acidity of a substance. It ranges from 0 to 14, with acids ranging from 0 to 7, 7 being neutral, and bases ranging from 7 to 14. The [H+] is the concentration of hydrogen ions, and is measured in moles per liter. The more hydrogen ions, then smaller the pH (notice the negative sign in front of the log) and the more acidity the solution is.
Notice that the Exponential Growth and Logarithmic models increase without bound to the right. The Gaussian and Exponential Decay models both approach the x-axis to the right. Only the Logistics Growth model gives you an upper bound to the right. The Exponential Decay and Gaussian models can be made to have an upper bound by subtracting the exponential expression (thus making it decreasing instead of increasing) from one and multiplying by the upper bound