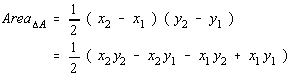Area of a Triangle

 

 Geometric Approach
Area of Rectangle Area of Rectangle
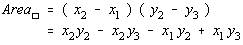Area of Triangle A

Technically, each of those distances should be the absolute value of the difference, but the problem is much easier to work without the absolute values.

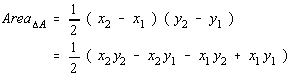 Area of Triangle A
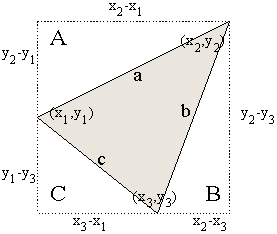
Area of Triangle B

Realize however, at if the points don't lie in the same positions (point 2 is the right most and upper most), that the area found using these formulas will be negative.

 Area of Triangle B
Area of Triangle C

For that reason, caution should be exerted to always make the final answer non-negative. The area of a triangle, after all, can't be negative.

 Area of Triangle C
Let's add the areas of the three outside triangles together. Area of Outside Triangles
SimplifyingArea of Outside Triangles
Now, to subtract the areas of the three triangles from the area of the rectangle.
Area of Triangle
Simplifying Area of Triangle
Let's regroup those termsArea of Triangle
Wow, quite an exercise, isn't it?
Now, consider the determinant formed by placing the x-coordinates in the first column, the y-coordinates in the second column, and the constant 1 in the last column. Determinant
Let's evaluate the determinantExpansion of Determinant by expanding along the 3rd column.
Notice that this differs in the area of the triangle only in sign. The reason for this is because of the order the points were chosen in. If the points were chosen to be points 1, 2, and 3 in a different order, then the determinant would change only in sign. (Recall that interchanging two rows changes the sign of the determinant).