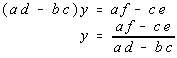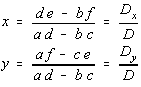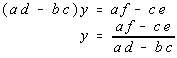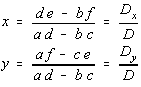Cramer's Rule

Let's solve a generic 2x2 system of linear equations.
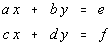To solve for x, let's eliminate the y's by multiplying the top equation by d and the bottom equation by -b
When you add the two equations together, and solve for x, you get
Now, let's solve for y by eliminating the x's. Multiply the top equation by -c and the bottom equation by a.
When you add the two equations together, and solve for y, you get
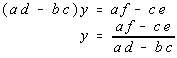Now, consider the following definitions
The determinant D formed by taking the coefficients
The determinant Dx formed by taking the coefficient matrix and replacing the x's by the constants on the right hand side.
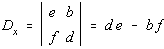The determinant Dy formed by taking the coefficient matrix and replacing the y's by the constants on the right hand side.
Have you seen those determinants anywhere before? If not, then you've not been reading the lecture notes.
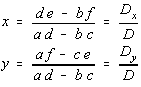