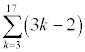
An arithmetic sequence is a sequence in which the difference between consecutive terms is constant.
Since this difference is common to all consecutive pairs of terms, it is called the common difference. It is denoted by d. If the difference in consecutive terms is not constant, then the sequence is not arithmetic. The common difference can be found by subtracting two consecutive terms of the sequence.
The formula for the common difference of an arithmetic sequence is: d = an+1 - an
An arithmetic sequence is a linear function. Instead of y=mx+b, we write an=dn+c where d is the common difference and c is a constant (not the first term of the sequence, however).
A recursive definition, since each term is found by adding the common difference to the previous term is ak+1=ak+d.
For any term in the sequence, we've added the difference one less time than the number of the term. For example, for the first term, we haven't added the difference at all (0 times). For the second term, we've added the difference once. For the third term, we've added the difference two times.
The formula for the general term of an arithmetic sequence is: an = a1 + (n-1) d
A series is a sum of a sequence. We want to find the nth partial sum or the sum of the first n terms of the sequence. We will denote the nth partial sum as Sn.
Consider the arithmetic series S5 = 2 + 5 + 8 + 11 + 14. There is an easy way to calculate the sum of an arithmetic series.
S5 = 2 + 5 + 8 + 11 + 14
The key is to switch the order of the terms. Addition is commutative, so changing the order doesn't change the sum.
S5 = 14 + 11 + 8 + 5 + 2
Now, add those two equations together.
2*S5 = (2+14) + (5+11) + (8+8) + (11+5) + (14+2)
Notice that each of those sums on the right hand side is 16. Instead of writing 16 (the sum of the first and last terms) five times, we can write it as 5 * 16 or 5 * (2 + 14)
2*S5 = 5*(2 + 14)
Finally, divide the whole thing by 2 to get the sum and not twice the sum
S5 = 5/2 * (2 + 14)
I've purposely not simplified the 2+14 so that you can see where the numbers come from. This sum would be 5/2 *(16) = 5(8) = 40.
Now, if we try to figure out where the different parts of that formula come from, we can conjecture about a formula for the nth partial sum. The 5 is because there were five terms, n. The 16 is the sum of the first and last terms, a1 + an. The 2 is because we added the sum twice and will remain a 2. Therefore, the sum of the first n terms of an arithmetic sequence is Sn=n/2*(a1+an)
There is another formula that is sometimes used for the nth partial sum of an arithmetic sequence. It is obtained by substituting the formula for the general term into the above formula and simplifying. The preferred method is to go ahead and find the nth term, and then just plug that number into the formula.
Sn = n/2 * ( 2a1 + (n-1) d )
Find the sum from k=3 to 17 of (3k-2).
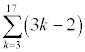
The first term is found by substituting k=3 into 3k-2 to get 7. The last term is 3(17)-2 = 49. There are 17 - 3 + 1 = 15 terms. So, the sum is 15 / 2 * (7 + 49) = 15 / 2 * 56 = 420.
Note that there are 15 terms there. When the lower limit of the summation is 1, there is little problem figuring out what the number of terms is. However, when the lower limit is any other number, it seems to give people difficulty. No one would argue that if you went from 1 to 10, there are 10 numbers. However, the difference between 10 and 1 is only 9. So, when you are finding the number of terms, it is the upper limit minus the lower limit plus one.