2.4 - Solving Equations Algebraically

Quadratic Equations

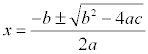
A quadratic equation is an equation that can be written as Ax² + Bx + C = 0 where A≠0. This form is called the standard form.

There are four ways to solve a quadratic equation.

Factoring

Works well when the quadratic can easily be factored.

Some of you were taught the trial and error method of factoring. Others of you were taught the AC Method of Factoring. The AC Method is explained elsewhere if you want to review or learn it.

The idea behind factoring is to place the equation into standard form, and then factor the left hand side into two factors (x-a) and (x-b). The solutions to the equation are then x=a and x=b. The factors will of course vary if A≠1. Factoring works because there is a rule which says if the product of two factors is zero, then one of the factors must be zero.

Extraction of Roots

Works well when there is no linear term, that is, when B=0.

The extraction of roots is called the square root principle by your text. The goal here is to get the squared variable term by itself on one side and a non-negative constant on the other side.

The square root of both sides is then taken. Remember that the square root of x² is the absolute value of x. When you solve an equation involving an absolute value, you will get a plus and minus in the solution. Too often, we bypass the step with the absolute value in it and go straight to the plus/minus phase. This is okay, as long as we remember the reason.

Completing the Square

Works well when the leading coefficient A is 1 and B is even.

1. If A is not 1, then either divide every term by A so that it is 1 or factor an A out of the variable terms only (not out of the constant).
2. Move the constant to the right hand side. Be sure and leave space at the end of the left hand side before the equal sign for the constant which will be inserted in there later.
3. Take 1 / 2 of the linear coefficient (B) and call that number "b". On the next line, write (x+b)² =. We will fill in the right hand side later. Of course, if B is negative, then the expression will look like (x-b)² =.
4. Square that value you just found (one-half of B) and write it in that space you left at the end of the left hand side before the equal sign on the previous line. Add the same value to the right hand side, also. It is very important that we add the same thing to both sides. If you chose to factor out the A, rather than dividing through by it, make sure that you add A times that constant to the right hand side.
5. Simplify the right hand side
6. Continue the process as an extraction of roots problem.

Quadratic Formula

Works well when the moon is aligned with Jupiter. Not actually, just seeing if anyone bothers to read these notes.

The quadratic formula is a catch-all that can be used to solve any quadratic equation. The equation must first of all be written in standard form, and then the coefficients plugged into the formula. The formula was derived in class by completing the square on a generic quadratic equation.

if ax² + bx + c = 0 and a ≠ 0, then x = ( -b +/- sqrt (b² - 4ac ) ) / ( 2a )

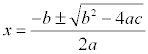
If the solutions from the quadratic formula are rational (no radicals), then the equation could have been solved by factoring.

Discriminant b²-4ac

The discriminant is the radicand from the radical in the quadratic formula. Depending on what type of number the discriminant is, we can tell what type and how many solutions there will be.

Polynomials of Higher Degree

Try factoring. Be sure to check for a greatest common factor first.

Equations involving Radicals

1. Isolate the radical term on one side.
2. Square both sides of the equation. Warning! Squaring is not a one-to-one function and you may introduce extraneous solutions. Also, don't forget that there is a middle term when squaring a binomial.
3. Solve for x.
4. Check your answers. There may be extraneous solutions.

Equations with more than one radical term

1. Isolate one of the radical terms on one side. It doesn't matter which one. Do NOT square both sides of the equation if both radicals are on the same side of the equal sign. It will work out if you are careful, but it will be extremely messy.
2. Square both sides of the equation.
3. Simplify.
4. Isolate the remaining radical on a side by itself. Remember there will be a radical because of the middle term when you square a binomial.
5. Square both sides again.
6. Solve for x.
7. Check your answers. Really important here. You applied a non 1-1 function twice and so there really could be extraneous solutions. Be sure to check.

Equations involving Fractions

Fractions are indeed your friends. Sometimes. When you need to give a solution, they are preferred over decimals. If you have the choice as to working with decimals or working with fractions, always choose the fraction if the decimals do not terminate. However, if you have the option, and you do with equations, of not working with either one - take it!

1. Find the least common denominator (LCD).
2. Set the LCD = 0 and note what values of x cannot be used. We will be eliminating the denominators in the next step and the domain will no longer be implied, therefore it is necessary to state the restrictions. I told you this all fit together.
3. Multiply every term of both sides by the LCD and simplify.
4. Check your answer against your restrictions to make sure you're not using an extraneous solution.

Equations involving Absolute Value

There are two possible values which have the same absolute value. Remember, the absolute value is a piece-wisely defined function. Therefore, when solving an equation containing an absolute value you must create two equations, one for each piece.

Also note the restrictions when you break the equation up into its two parts. It is possible to get extraneous solutions (see problem 102). If you don't want to take the time to keep track of the restrictions, then 1) don't be surprised when you miss the problem on the exam or 2) check all of your solutions back into the original equation.

Position Equation

The height, s, in feet of a freely falling body (near the surface of the earth), after t seconds, can be modeled by the function given.

s(t) = -16 t² + v₀t + s₀

v₀ = initial velocity and s₀ = initial height

The -16 is valid for the earth's surface and will change depending on the celestial body exerting the gravitational pull. For those interested, the quadratic coefficient will always be one-half the acceleration due to gravity (-32 ft/s/s on the earth). The rest of the equation is valid no matter what body you're on.