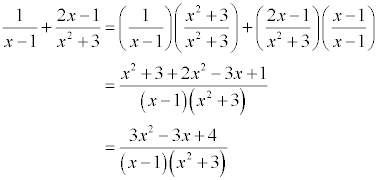In
algebra, you have carried that
process on to addition of rational
expressions. You once again multiplied the numerator and denominator of each
term by what was missing from the denominator of that term.In arithmetic, you learned how to add fractions. You found the least common denominator, and then multiplied both the numerator and denominator of each term by what was needed to complete the common denominator.
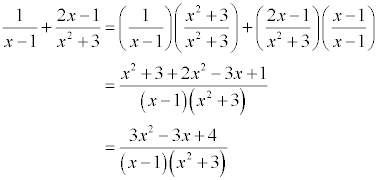In
algebra, you have carried that
process on to addition of rational
expressions. You once again multiplied the numerator and denominator of each
term by what was missing from the denominator of that term.
With Partial Fraction Decomposition, we're going to reverse the process and decompose a rational expression into two or more simpler proper rational expressions that were added together.
Partial Fraction Decomposition only works for proper rational expressions, that is, the degree of the numerator must be less than the degree of the denominator. If it is not, then you must perform long division first, and then perform the partial fraction decomposition on the rational part (the remainder over the divisor). After you've done the partial fraction decomposition, just add back in the quotient part from the long division.
When discussing polynomials in section 3.4, we learned that every polynomial with real coefficients can be factored using only linear and irreducible quadratic factors. This means that there are only two types of factors that we have to worry about.
If the partial fractions we're decomposing the rational expression into must be proper, then the only thing that can be over a linear factor is a constant. So, for every linear factor in the denominator, you will need a constant in over that in the numerator.
If the partial fractions we're decomposing the rational expression into must be proper, then an irreducible quadratic factor could have a linear term and/or a constant term in the numerator. So, for every irreducible quadratic factor in the denominator, you will need a linear term and a constant term in the numerator.
Consider a fraction in which the denominator is 8. Does that mean that the denominator of each term being added together had to be an 8? No, the denominators could have been 2, 4, or 8 because the common denominator between 2, 4, and 8 is 8. The implications of this for partial fraction decomposition are that when you have a repeated factor (a factor with a multiplicity other than one), you need to include a factor in the expansion for each power possible.
For example, if you have an (x-2)3, you will need to include an (x-2), an (x-2)2, and an (x-2)3.
The exponents of 2 or 3 does not change whether the factor is linear or quadratic, only how many times the factor is there. Each of those (x-2) factors would receive a constant term in the numerator because x-2 is linear, no matter what power it is raised to.
A proper fraction is a fraction where the numerator is less than the denominator. For rational expressions, that means the degree in the numerator is less than the degree in the denominator. If you have an improper fraction, you first have to perform long division to get a quotient and a remainder.
Leave the quotient part alone, but perform the partial fraction decomposition on the fraction that remained.
After setting up the partial fraction equation, you multiply both sides of the equation by the least common denominator to get rid of the fractions. The resulting equation, without the fractions, is called the Basic Equation.
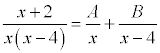When there are linear factors, the easiest way to do the
decomposition is probably to pick nice values for x.
In the example to the right, we take each factor in the denominator and give it its own term on the right side. Since each factor in the denominator is linear and the rational expressions need to be proper, a constant term was placed in each numerator of each term. We multiply through by the least common denominator to arrive at the equation without the fractions. This equation is called the Basic Equation and is ...
x + 2 = A ( x - 4 ) + B x
"Nice" values for x are those that cause each linear factor to be zero. In this case, x=4 and x=0 are nice. "Nice" values will cause every term except for one to drop out of the equation, and so you will be able to find the value of a variable very quickly.
When you let x = 0, the B term drops out and you get ...
0 + 2 = A ( 0 - 4 ) or 2 = -4A. Solving that gives A = -1/2.
When you let x = 4, the A term drops out and you get ...
4 + 2 = B ( 4 ) or 6 = 4B. Solving that gives B = 3/2.
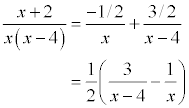After
you have found the values of each constant, it is important that you plug those
values back into the
decomposition. Don't just stop with A=-1/2, B=3/2 because someone else may have
defined A and B differently. The correct answer is to place them back into
the decomposition
and simplify if necessary. The simplification would be to
reduce the number of signs (don't have the first term negative if possible) and
to eliminate the compound fractions by factoring out the least common denominator
of the numerators.
Note: There are only as many nice values as there are distinct (different) linear factors. If there are repeated linear factors or irreducible quadratic factors (repeated or not), you will not have enough "nice" values to pick. In cases like that, you will have to pick convenient but not-so-nice values and then substitute the known constants into the equation to find the other constants. Plug in easy numbers like x=0, x=1, etc.
You will need to pick as many values for x as there are constants to be found.
The first technique of picking values for x works extremely well when all the factors are distinct linear factors. If there are any linear factors, then first method is still probably the better technique to use. However, if there are only irreducible quadratic factors, then the method of picking values for x can become messy.
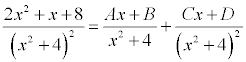There is another way to do these
problems (actually, this technique will
work when there are linear factors, just
that the other is easier and faster).
The first part of the process is the same. Go ahead and write out the decomposition, including constant terms over linear factors and linear and constant terms over the irreducible quadratic factors. Then, multiply through by the least common denominator to find the basic equation. That much is the same. The basic equation is ...
2x2 + x + 8 = Ax (x2 + 4) + B (x2+4) + Cx + D
Now the difference comes.
Go ahead and expand (multiply out) the basic equation ...
2x2 + x + 8 = Ax3 + 4Ax + Bx2+ 4B + Cx + D
and regroup the terms by common powers of the variable x.
2x2 + x + 8 = Ax3 + Bx2 + 4Ax + Cx + 4B + D
Now factor out the x's by power.
2x2 + x + 8 = ( A ) x3 + ( B ) x2 + ( 4A + C ) x + ( 4B + D ) (1)
The next part works because if two polynomials are going to be equal, they must have the same number of similar terms on both sides. So the trick here is to equate both sides of the equation together by equating similar terms.
Set the x3 terms on the left (of which there are none) equal to the x3 terms on the right (of which there are A) to arrive at the first equation 0=A. Well, that was pretty easy, and already you have the value for A.
Set the x2 terms on the left (of which there are 2) equal to the x2 terms on the right (of which there are B) to arrive at the second eqation of 2=B. Now you know B.
For the x's, there is 1 on the left and 4A+C on the right, so 1=4A+C.
For the constants, there are 8 on the left and 4B+D on the right, so 8=4B+D.
You may have to solve a system of linear equations, but that's why this section on partial fractions is in this chapter. We just refreshed our memories on how to solve a system of linear equations in the last section.
After
some solving, we arrive at A=0, B=2, C=1, and D=0 and we are ready
to plug those values back into
the original decomposition to arrive at the final answer.
Be sure and simplify the answer if necessary.
This example was actually pretty easy because you were able to find A and B right off the bat. Many times, you will need to solve a much larger system of equations to find the values.