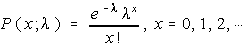
A multinomial experiment is an extended binomial probability. The difference is that in a multinomial experiment, there are more than two possible outcomes. However, there are still a fixed number of independent trials, and the probability of each outcome must remain constant from trial to trial.
Instead of using a combination, as in the case of the binomial probability, the number of ways the outcomes can occur is done using distinguishable permutations.
An example here will be much more useful than a formula.
The probability that a person will pass a College Algebra class is 0.55, the probability that a person will withdraw before the class is completed is 0.40, and the probability that a person will fail the class is 0.05. Find the probability that in a class of 30 students, exactly 16 pass, 12 withdraw, and 2 fail.
| Outcome | x | p(outcome) |
| Pass | 16 | 0.55 |
| Withdraw | 12 | 0.40 |
| Fail | 2 | 0.05 |
| Total | 30 | 1.00 |
The probability is found using this formula:
30!
P = ---------------- * 0.55^16 * 0.40^12 * 0.05^2
(16!) (12!) (2!)
You can do this on the TI-82.
Named after the French mathematician Simeon Poisson, Poisson probabilities are useful when there are a large number of independent trials with a small probability of success on a single trial and the variables occur over a period of time. It can also be used when a density of items is distributed over a given area or volume.
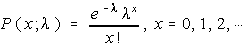
Lambda in the formula is the mean number of occurrences. If you're approximating a binomial probability using the Poisson, then lambda is the same as mu or n * p.
If there are 500 customers per eight-hour day in a check-out lane, what is the probability that there will be exactly 3 in line during any five-minute period?
The expected value during any one five minute period would be 500 / 96 = 5.2083333. The 96 is because there are 96 five-minute periods in eight hours. So, you expect about 5.2 customers in 5 minutes and want to know the probability of getting exactly 3.
p(3;500/96) = e^(-500/96) * (500/96)^3 / 3! = 0.1288 (approx)
Hypergeometric experiments occur when the trials are not independent of each other and occur due to sampling without replacement -- as in a five card poker hand.
Hypergeometric probabilities involve the multiplication of two combinations together and then division by the total number of combinations.
How many ways can 3 men and 4 women be selected from a group of 7 men and 10 women?
The answer is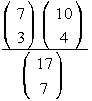 = 7350/19448 = 0.3779 (approx)
= 7350/19448 = 0.3779 (approx)
Note that the sum of the numbers in the numerator are the numbers used in the combination in the denominator.
This can be extended to more than two groups and called an extended hypergeometric problem.
You can use the TI-82 to find hypergeometric probabilities.