Stats - Normal Distributions

---

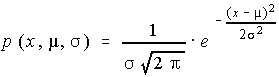
Any Normal Distribution

• Bell-shaped
• Symmetric about mean
• Continuous
• Never touches the x-axis
• Total area under curve is 1.00
• Approximately 68% lies within 1 standard deviation of the mean, 95% within 2 standard deviations, and 99.7% within 3 standard deviations of the mean. This is the Empirical Rule mentioned earlier.
• Data values represented by x which has mean mu and standard deviation sigma.
• Probability Function given by

Standard Normal Distribution

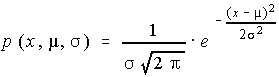
Same as a normal distribution, but also ...

• Mean is zero
• Variance is one
• Standard Deviation is one
• Data values represented by z.
• Probability Function given by

Normal Probabilities

Comprehension of this table is vital to success in the course!

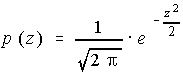
There is a table which must be used to look up standard normal probabilities. The z-score is broken into two parts, the whole number and tenth are looked up along the left side and the hundredth is looked up across the top. The value in the intersection of the row and column is the area under the curve between zero and the z-score looked up.

Because of the symmetry of the normal distribution, look up the absolute value of any z-score.

Computing Normal Probabilities

There are several different situations that can arise when asked to find normal probabilities.

Situation	Instructions
Between zero and any number	Look up the area in the table
Between two positives, or Between two negatives	Look up both areas in the table and subtract the smaller from the larger.
Between a negative and a positive	Look up both areas in the table and add them together
Less than a negative, or Greater than a positive	Look up the area in the table and subtract from 0.5000
Greater than a negative, or Less than a positive	Look up the area in the table and add to 0.5000

This can be shortened into two rules.

1. If there is only one z-score given, use 0.5000 for the second area, otherwise look up both z-scores in the table
2. If the two numbers are the same sign, then subtract; if they are different signs, then add. If there is only one z-score, then use the inequality to determine the second sign (< is negative, and > is positive).

Finding z-scores from probabilities

This is more difficult, and requires you to use the table inversely. You must look up the area between zero and the value on the inside part of the table, and then read the z-score from the outside. Finally, decide if the z-score should be positive or negative, based on whether it was on the left side or the right side of the mean. Remember, z-scores can be negative, but areas or probabilities cannot be.

Situation	Instructions
Area between 0 and a value	Look up the area in the table Make negative if on the left side
Area in one tail	Subtract the area from 0.5000 Look up the difference in the table Make negative if in the left tail
Area including one complete half (Less than a positive or greater than a negative)	Subtract 0.5000 from the area Look up the difference in the table Make negative if on the left side
Within z units of the mean	Divide the area by 2 Look up the quotient in the table Use both the positive and negative z-scores
Two tails with equal area (More than z units from the mean)	Subtract the area from 1.000 Divide the area by 2 Look up the quotient in the table Use both the positive and negative z-scores

Using the table becomes proficient with practice, work lots of the normal probability problems!