Stats: Estimating the Mean
You are estimating the population mean, mu, not the sample mean, x bar.
Population Standard Deviation Known
If the population standard deviation, sigma is known, then the mean has a normal (Z) distribution.
The maximum error of the estimate is given by the formula for E shown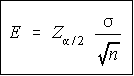 .
The Z here is the z-score obtained from the normal table, or the bottom of the t-table as
explained in the introduction to estimation. The z-score is a factor of the
level of confidence, so you may get in the habit of writing it next to the
level of confidence.
.
The Z here is the z-score obtained from the normal table, or the bottom of the t-table as
explained in the introduction to estimation. The z-score is a factor of the
level of confidence, so you may get in the habit of writing it next to the
level of confidence.
Once you have computed E, I suggest you save it to the memory on your calculator. On the TI-82, a good choice would be the letter E. The reason for this is that the limits for the confidence
interval are now found by subtracting and adding the maximum error of the estimate from/to the
sample mean.
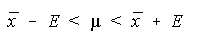
When the population standard deviation is unknown, the mean has a Student's t distribution. The
Student's t distribution was created by William T. Gosset, an Irish brewery worker. The brewery
wouldn't allow him to publish his work under his name, so he used the pseudonym "Student".
The Student's t distribution is very similar to the standard normal distribution.
- It is symmetric about its mean
- It has a mean of zero
- It has a standard deviation and variance greater than 1.
- There are actually many t distributions, one for each degree of freedom
- As the sample size increases, the t distribution approaches the normal distribution.
- It is bell shaped.
- The t-scores can be negative or positive, but the probabilities are always positive.
Degrees of Freedom
A degree of freedom occurs for every data value which is allowed to vary once a statistic has been
fixed. For a single mean, there are n-1 degrees of freedom. This value will change depending on
the statistic being used.
Population Standard Deviation Unknown
If the population standard deviation, sigma is unknown, then the mean has a student's t (t)
distribution and the sample standard deviation is used instead of the population standard
deviation.
The maximum error of the estimate is given by the formula for E shown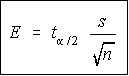 .
The t here is the t-score obtained from the Student's t table. The t-score
is a factor of the level of confidence and the sample size.
.
The t here is the t-score obtained from the Student's t table. The t-score
is a factor of the level of confidence and the sample size.
Once you have computed E, I suggest you save it to the memory on your
calculator. On the TI-82, a good choice would be the letter E. The reason for this is that the
limits for the confidence interval are now found by subtracting and adding the maximum error of
the estimate from/to the sample mean.
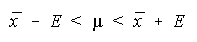
Notice the formula is the same as for a population mean when the population standard deviation is
known. The only thing that has changed is the formula for the maximum error of the estimate.
Table of Contents
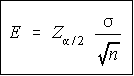 .
The Z here is the z-score obtained from the normal table, or the bottom of the t-table as
explained in the introduction to estimation. The z-score is a factor of the
level of confidence, so you may get in the habit of writing it next to the
level of confidence.
.
The Z here is the z-score obtained from the normal table, or the bottom of the t-table as
explained in the introduction to estimation. The z-score is a factor of the
level of confidence, so you may get in the habit of writing it next to the
level of confidence.
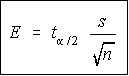 .
The t here is the t-score obtained from the Student's t table
.
The t here is the t-score obtained from the Student's t table