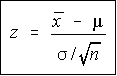If the population standard deviation, sigma, is known, then the population
mean has a normal distribution, and you will be using the z-score formula
for sample means. The test statistic is the standard formula you've seen
before.
You are testing mu, you are not testing x bar. If you knew the value of mu, then there would be
nothing to test.
All hypothesis testing is done under the assumption the null hypothesis is true! |
I can't emphasize this enough. The value for all population parameters in the test statistics come from the null hypothesis. This is true not only for means, but all of the testing we're going to be doing.
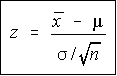If the population standard deviation, sigma, is known, then the population
mean has a normal distribution, and you will be using the z-score formula
for sample means. The test statistic is the standard formula you've seen
before.
The critical value is obtained from the normal table, or the bottom line from the t-table.
If the population standard deviation, sigma, is unknown, then the population
mean has a student's t distribution, and you will be using the t-score formula
for sample means. The test statistic is very similar to that for the z-score,
except that sigma has been replaced by s and z has been replaced by t.
The critical value is obtained from the t-table. The degrees of freedom for this test is n-1.
If you're performing a t-test where you found the statistics on the calculator (as opposed to being given them in the problem), then use the VARS key to pull up the statistics in the calculation of the test statistic. This will save you data entry and avoid round off errors.
Notice the general pattern of these test statistics is (observed - expected) / standard deviation.
