Stats: Coefficient of Determination

Coefficient of Determination

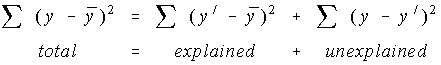
The coefficient of determination is ...

• the percent of the variation that can be explained by the regression equation.
• the explained variation divided by the total variation
• the square of r

What's all this variation stuff?

Every sample has some variation in it (unless all the values are identical, and that's unlikely to happen). The total variation is made up of two parts, the part that can be explained by the regression equation and the part that can't be explained by the regression equation.

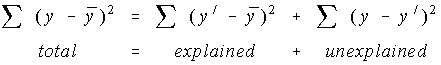
Well, the ratio of the explained variation to the total variation is a measure of how good the regression line is. If the regression line passed through every point on the scatter plot exactly, it would be able to explain all of the variation. The further the line is from the points, the less it is able to explain.

Coefficient of Non-Determination

The coefficient of non-determination is ...

• The percent of variation which is unexplained by the regression equation
• The unexplained variation divided by the total variation
• 1 - r^2

Standard Error of the Estimate

The coefficient of non-determination was used in the t-test to see if there was significant linear correlation. It was the in the numerator of the standard error formula.

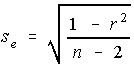The standard error of the estimate is the square root of the coefficient of non-determination divided by it's degrees of freedom.

Confidence Interval for y'

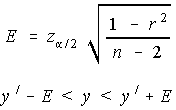The following only works when the sample size is large. Large in this instance is usually taken to be more than 100. We're not going to cover this in class, but is provided here for your information. The maximum error of the estimate is given, and this maximum error of the estimate is subtracted from and added to the estimated value of y.