Stats: Chi-Square Distribution
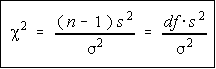 The chi-square (
The chi-square ( 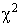 ) distribution is obtained from the
values of the ratio of the sample variance and population
variance multiplied by the degrees of freedom. This occurs
when the population is normally distributed with population
variance sigma^2.
) distribution is obtained from the
values of the ratio of the sample variance and population
variance multiplied by the degrees of freedom. This occurs
when the population is normally distributed with population
variance sigma^2.
Properties of the Chi-Square
- Chi-square is non-negative. Is the ratio of two non-negative values, therefore must be non-negative itself.
- Chi-square is non-symmetric.
- There are many different chi-square distributions, one for each degree of freedom.
- The degrees of freedom when working with a single population variance is n-1.
Since the chi-square distribution isn't symmetric, the method for looking up left-tail values is
different from the method for looking up right tail values.
- Area to the right - just use the area given.
- Area to the left - the table requires the area to the right, so subtract the given area from one
and look this area up in the table.
- Area in both tails - divide the area by two. Look up this area for the right critical value and
one minus this area for the left critical value.
DF which aren't in the table
When the degrees of freedom aren't listed in the table, there are a couple of choices that you
have.
- You can interpolate. This is probably the more accurate way. Interpolation involves
estimating the critical value by figuring how far the given degrees of freedom are between the
two df in the table and going that far between the critical values in the table. Most people born
in the 70's didn't have to learn interpolation in high school because they had calculators which
would do logarithms (we had to use tables in the "good old" days).
- You can go with the critical value which is less likely to cause you to reject in error (type I
error). For a right tail test, this is the critical value further to the right (larger). For a left tail
test, it is the value further to the left (smaller). For a two-tail test, it's the value further to the
left and the value further to the right. Note, it is not the column with the degrees of freedom
further to the right, it's the critical value which is further to the right. The Bluman text has this
wrong on page 422. The guideline is right, the instructions are wrong.
Table of Contents
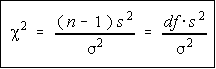 The chi-square (
The chi-square ( 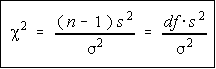 The chi-square (
The chi-square ( ![]() ) distribution is obtained from the
values of the ratio of the sample variance and population
variance multiplied by the degrees of freedom. This occurs
when the population is normally distributed with population
variance sigma^2.
) distribution is obtained from the
values of the ratio of the sample variance and population
variance multiplied by the degrees of freedom. This occurs
when the population is normally distributed with population
variance sigma^2.