Stats: One-Way ANOVA
A One-Way Analysis of Variance is a way to test the equality of three or more means at one time
by using variances.
Assumptions
- The populations from which the samples were obtained must be normally or approximately
normally distributed.
- The samples must be independent.
- The variances of the populations must be equal.
Hypotheses
The null hypothesis will be that all population means are equal, the alternative hypothesis is that at
least one mean is different.
In the following, lower case letters apply to the individual samples and capital letters apply to the
entire set collectively. That is, n is one of many sample sizes, but N is the total sample size.
Grand Mean
 The grand mean of a set of samples is the total of all the data values divided by
the total sample size. This requires that you have all of the sample data available
to you, which is usually the case, but not always. It turns out that all that is
necessary to find perform a one-way analysis of variance are the number of samples, the sample
means, the sample variances, and the sample sizes.
The grand mean of a set of samples is the total of all the data values divided by
the total sample size. This requires that you have all of the sample data available
to you, which is usually the case, but not always. It turns out that all that is
necessary to find perform a one-way analysis of variance are the number of samples, the sample
means, the sample variances, and the sample sizes.
 Another way to find the grand mean is to find the weighted average of the
sample means. The weight applied is the sample size.
Another way to find the grand mean is to find the weighted average of the
sample means. The weight applied is the sample size.
Total Variation
 The total variation (not variance) is comprised the sum of the
squares of the differences of each mean with the grand mean.
The total variation (not variance) is comprised the sum of the
squares of the differences of each mean with the grand mean.
There is the between group variation and the within group variation. The whole idea behind the
analysis of variance is to compare the ratio of between group variance to within group variance.
If the variance caused by the interaction between the samples is much larger when compared to
the variance that appears within each group, then it is because the means aren't the same.
Between Group Variation
 The variation due to the interaction between the samples is
denoted SS(B) for Sum of Squares Between groups. If the
sample means are close to each other (and therefore the Grand Mean) this will be small. There
are k samples involved with one data value for each sample (the sample mean), so there are k-1
degrees of freedom.
The variation due to the interaction between the samples is
denoted SS(B) for Sum of Squares Between groups. If the
sample means are close to each other (and therefore the Grand Mean) this will be small. There
are k samples involved with one data value for each sample (the sample mean), so there are k-1
degrees of freedom.
The variance due to the interaction between the samples is denoted MS(B) for Mean Square
Between groups. This is the between group variation divided by its degrees of freedom. It is also
denoted by 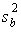 .
.
Within Group Variation
 The variation due to differences within individual samples, denoted
SS(W) for Sum of Squares Within groups. Each sample is considered
independently, no interaction between samples is involved. The degrees of freedom is equal to
the sum of the individual degrees of freedom for each sample. Since each sample has degrees of
freedom equal to one less than their sample sizes, and there are k samples, the total degrees of
freedom is k less than the total sample size: df = N - k.
The variation due to differences within individual samples, denoted
SS(W) for Sum of Squares Within groups. Each sample is considered
independently, no interaction between samples is involved. The degrees of freedom is equal to
the sum of the individual degrees of freedom for each sample. Since each sample has degrees of
freedom equal to one less than their sample sizes, and there are k samples, the total degrees of
freedom is k less than the total sample size: df = N - k.
The variance due to the differences within individual samples is denoted MS(W) for Mean Square
Within groups. This is the within group variation divided by its degrees of freedom. It is also
denoted by  . It is the weighted average of the variances (weighted with the degrees of
freedom).
. It is the weighted average of the variances (weighted with the degrees of
freedom).
F test statistic
 Recall that a F variable is the ratio of two independent chi-square variables
divided by their respective degrees of freedom. Also recall that the F test
statistic is the ratio of two sample variances, well, it turns out that's exactly what
we have here. The F test statistic is found by dividing the between group
variance by the within group variance. The degrees of freedom for the
numerator are the degrees of freedom for the between group (k-1) and the
degrees of freedom for the denominator are the degrees of freedom for the within group (N-k).
Recall that a F variable is the ratio of two independent chi-square variables
divided by their respective degrees of freedom. Also recall that the F test
statistic is the ratio of two sample variances, well, it turns out that's exactly what
we have here. The F test statistic is found by dividing the between group
variance by the within group variance. The degrees of freedom for the
numerator are the degrees of freedom for the between group (k-1) and the
degrees of freedom for the denominator are the degrees of freedom for the within group (N-k).
Summary Table
All of this sounds like a lot to remember, and it is. However, there is a table which makes things
really nice.
|
SS |
df |
MS |
F |
| Between
|
SS(B) |
k-1 |
SS(B)
-----------
k-1 |
MS(B)
--------------
MS(W) |
| Within
|
SS(W) |
N-k |
SS(W)
-----------
N-k |
. |
| Total
|
SS(W) + SS(B) |
N-1 |
. |
. |
Notice that each Mean Square is just the Sum of Squares divided by its degrees of freedom, and
the F value is the ratio of the mean squares. Do not put the largest variance in the numerator,
always divide the between variance by the within variance. If the between variance is smaller than
the within variance, then the means are really close to each other and you will fail to reject the
claim that they are all equal. The degrees of freedom of the F-test are in the same order they
appear in the table (nifty, eh?).
Decision Rule
The decision will be to reject the null hypothesis if the test statistic from the table is greater than
the F critical value with k-1 numerator and N-k denominator degrees of freedom.
If the decision is to reject the null, then at least one of the means is different. However, the
ANOVA does not tell you where the difference lies. For this, you need another test, either the
Scheffe' or Tukey test.
TI-82
Ok, now for the really good news. There's a program called ANOVA for the TI-82 calculator
which will do all of the calculations and give you the values that go into the table for you. You
must have the sample means, sample variances, and sample sizes to use the program. If you have
the sum of squares, then it is much easier to finish the table by hand (this is what we'll do with the
two-way analysis of variance)
Table of Contents
 The grand mean of a set of samples is the total of all the data values divided by
the total sample size. This requires that you have all of the sample data available
to you, which is usually the case, but not always. It turns out that all that is
necessary to find perform a one-way analysis of variance are the number of samples, the sample
means, the sample variances, and the sample sizes.
The grand mean of a set of samples is the total of all the data values divided by
the total sample size. This requires that you have all of the sample data available
to you, which is usually the case, but not always. It turns out that all that is
necessary to find perform a one-way analysis of variance are the number of samples, the sample
means, the sample variances, and the sample sizes.
 Another way to find the grand mean is to find the weighted average of the
sample means. The weight applied is the sample size.
Another way to find the grand mean is to find the weighted average of the
sample means. The weight applied is the sample size.
 Recall that a F variable is the ratio of two independent chi-square variables
divided by their respective degrees of freedom. Also recall that the F test
statistic is the ratio of two sample variances, well, it turns out that's exactly what
we have here. The F test statistic is found by dividing the between group
variance by the within group variance. The degrees of freedom for the
numerator are the degrees of freedom for the between group (k-1) and the
degrees of freedom for the denominator are the degrees of freedom for the within group (N-k).
Recall that a F variable is the ratio of two independent chi-square variables
divided by their respective degrees of freedom. Also recall that the F test
statistic is the ratio of two sample variances, well, it turns out that's exactly what
we have here. The F test statistic is found by dividing the between group
variance by the within group variance. The degrees of freedom for the
numerator are the degrees of freedom for the between group (k-1) and the
degrees of freedom for the denominator are the degrees of freedom for the within group (N-k).