Craps
The Game
Craps is a dice game where two dice are rolled and the sum of the dice determines
the outcome.
- If the sum is a 7 or 11, you win and the game is over.
- If the sum is a 2, 3, or 12, you lose and the game is over.
- If you roll a 4, 5, 6, 8, 9, or 10, that value becomes your "point"
and you continue to roll until you re-roll your point or a 7. If you roll
your point, you win; if you roll a 7, you lose.
Video: Use Real Player to listen to the instructions and
watch several games to make sure you understand the game. (56k
- DSL/Cable)
Some of the probabilities are easy to find. The fundamental counting principle
tells us there are 6*6=36 ways to roll two dice, all of them equally likely
if the dice are fair. There is only one way to roll a sum of 2 (snake eyes or
a 1 on both dice), so the probability of getting a sum of 2 is 1/36. There are
4 ways to get a five (1-4, 2-3, 3-2, 4-1) so the probability of getting a five
is 4/36. The probabilities of obtaining any of the first roll sums can be found
fairly easily and are shown in the table below.
Probabilities of Sum on First Roll
| Sum |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| Probability |
1/36 |
2/36 |
3/36 |
4/36 |
5/36 |
6/36 |
5/36 |
4/36 |
3/36 |
2/36 |
1/36 |
We can find the probability of winning, losing, or obtaining a point on the
first roll of the game by adding up the probabilities for the sums that go with
winning, losing, or getting a point. For example, since a 7 or an 11 is a winner
on the first roll and their probabilities are 6/36 and 2/36, the probability
of winning on the first roll is 6/36+2/36=8/36.
Probabilities of Winning, Losing, or Getting a Point on First Roll
| Outcome |
Win |
Lose |
Point |
| Probability |
8/36 |
4/36 |
24/36 |
The Point
The main problem with game of craps is that it can theoretically go on forever
when a point is obtained on the first roll. Now, in actual practice, it doesn't.
Eventually, you are going to either re-roll that point and win or roll a 7 and
lose.
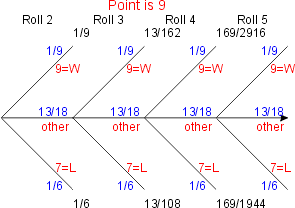 But,
becasue you could theoretically go on forever, finding the probabilities involve
an infinite geometric series. As an example, consider the case when the point
is a 9 that is shown in the tree diagram to the right. Once you roll a 9, there
is a 4/36=1/9 chance of rolling it again on any roll and a 6/36=1/6 chance of
rolling a 7 and losing. However, there is a 13/18 chance that you will roll
neither and the game will continue for another round.
But,
becasue you could theoretically go on forever, finding the probabilities involve
an infinite geometric series. As an example, consider the case when the point
is a 9 that is shown in the tree diagram to the right. Once you roll a 9, there
is a 4/36=1/9 chance of rolling it again on any roll and a 6/36=1/6 chance of
rolling a 7 and losing. However, there is a 13/18 chance that you will roll
neither and the game will continue for another round.
There is a 1/9 chance of winning on the second roll (the first after the point),
a 13/18*1/9=13/162 chance of winning on the third roll, a 13/18*13/18*1/9=169/2916
chance of winning on the fourth roll. But it doesn't stop there, it keeps going,
and going, and going. Then you have to add all those probabilities up and that
involves an infinite geometric series. That might not be difficult for you,
but since the prerequisite for the applied statistics course is just intermediate
algebra, most of the students have never seen an infinite geometric series.
So, there has to be another way.
The Simulation
This is a game that is most fun when it is simulated using actual dice. Sure,
it would be possible and quicker to simulate it using a computer, but it wouldn't
be nearly as fun.
Here's how the simulation works. Roll a pair of dice and record the sum in
the table where it says "Sum on first roll". We are then going to
record the result of the first roll as "Win", "Lose", or
"Point" in the table where it says "Result of first roll".
If the sum is a 2, 3, 7, 11, or 12, go ahead and copy the first roll results
into the overall results column and move on to the next game. If you have rolled
a point, continue to roll the die until you roll either that point or a 7, but
do not record the value of each of those rolls. Once you have rolled your point
or a 7, then record either "Win" or "Lose" in the table
for the overall results. You may wish to abbreviate the results as "W",
"L", or "P".
| Game |
Sum on first roll |
Result of first roll |
Overall Result |
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
| 5 |
|
|
|
The Analysis
After you have played several games (I recommend 36 since there are 36 different
outcomes possible and it makes the probabilities nicer), it's time to sit back
and look at what you have gathered.
First Roll Probabilities
Go through and count how many times each sum appeared as the first roll of
the dice. Record it in the table below as a fraction over the total number of
rolls and compare it to the theoretical probabilities we found earlier.
| Sum |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| Observed |
|
|
|
|
|
|
|
|
|
|
|
| Theoretical |
1/36 |
2/36 |
3/36 |
4/36 |
5/36 |
6/36 |
5/36 |
4/36 |
3/36 |
2/36 |
1/36 |
Are the observed probabilities close to the theoretical probabilities? They
should get closer as you simulate more crap games (law of large numbers).
First Roll Outcomes
Now add the number of times you got a win, lose, or point on the first roll
of the dice and write that as a fraction. If you played the game right, this
can also be found by adding the probabilities of getting a win (7 or 11), lose
(2, 3, or 12), or point (all else) together.
Record them in the table below and compare them with the theoretical probabilities
found by adding the theoretical probabilities as mentioned in the last paragraph
or that we found earlier in this document.
| Outcome |
Win |
Lose |
Point |
| Observed |
|
|
|
| Theoretical |
8/36 |
4/36 |
24/36 |
Final Results
You're probably thinking to yourself that this has been pointless. So far,
we haven't found anything that we couldn't find through simple probabilities
and it was much quicker and more accurate (exact instead of an approximation).
What we're really interested in finding is the final outcomes of the game;
that is, the probabilities of winning or losing the whole game. Count how many
times you won and lost for the overall results and write that as a fraction
over the total.
| Outcome |
Win |
Lose |
| Observed |
|
|
| Theoretical |
244/495 |
251/495 |
Did your results come out close to the theoretical results (found using infinite
geometric series or absorbing markov chains)? You should have lost a few more
games than you won. Well, after all, the casinos want to make money, don't they?
Type of Simulation
This is a simulation used to find probabilities. In this kind of simulation,
you conduct an experiment and ultimately find the number of successes divided
by the number of trials to find the relative frequency or the empirical probability.
Success is defined as whatever you're trying to find the probability of. So,
if you're looking for the probability of rolling a 6, then it is the number
of 6's over the total number of rolls. If you're trying to find the probability
of losing the game, then it is the number of losses divided by the total number
of games.
Return to Simulation Page
 But,
becasue you could theoretically go on forever, finding the probabilities involve
an infinite geometric series. As an example, consider the case when the point
is a 9 that is shown in the tree diagram to the right. Once you roll a 9, there
is a 4/36=1/9 chance of rolling it again on any roll and a 6/36=1/6 chance of
rolling a 7 and losing. However, there is a 13/18 chance that you will roll
neither and the game will continue for another round.
But,
becasue you could theoretically go on forever, finding the probabilities involve
an infinite geometric series. As an example, consider the case when the point
is a 9 that is shown in the tree diagram to the right. Once you roll a 9, there
is a 4/36=1/9 chance of rolling it again on any roll and a 6/36=1/6 chance of
rolling a 7 and losing. However, there is a 13/18 chance that you will roll
neither and the game will continue for another round.