Math 160 - Projects
Listed below are the various projects that will be assigned throughout
the semester. These projects take you above and beyond the material covered
in the book or require outside data acquisition.
Each of these projects is worth 20 points and is due two class periods
after the scheduled lecture for the corresponding chapter is finished. Due
dates are noted on the class calendar.
You may work in groups of up to three people per project (with the
exception of the first part of the first project, which is an individual
project). Turn in one project with all group member's names on it.
Plan on reading the section of the book dealing with the matter before we
cover it in class; you will not always have time to finish the project if
you wait until we do.
Some of these projects are very similar to problems that will appear on
your exam. So even though they may not be due until after the exam, it would
be wise for you to work and understand them before the exam.
Project 1, Chapter 3
Part I (10 points) - Individual
Your project is to plan a retirement fund for yourself. To simplify
calculations, assume all transactions - starting of annuity fund,
retirement, and death - occur on your birthday. Assume a nominal interest
rate of 3% has been guaranteed for the remainder of your life. There is a
worksheet available to give you an idea of the
format I'm looking for. Feel free to use that paper to write your answers
on.
- Identify the age you will be on your birthday this year.
- Identify the age at which you wish to retire. Identify the number of
years before retirement.
- Identify the age at which you anticipate dying. Identify the number of
years of retirement.
- Identify the monthly payment you anticipate needing during your
retirement.
- Calculate the present value necessary on the date of retirement to
finance your retirement.
- The present value needed to retire is the future value necessary upon
retirement. Calculate the monthly payment needed before retirement to have
enough money to retire.
- Calculate the amount of money in your retirement fund after ten years
assuming you make the regular payments just calculated.
- After the ten years, assume that you receive an inheritance of $20,000
and add it to your retirement fund. If you stop making regular payments, and
just let what money is in the account draw interest, what will the amount be
at the time of retirement?
- Subtract this amount from the future value needed upon retirement and
recompute the monthly payment necessary to obtain the future value. Remember
that ten years have gone by. If no more monthly payments are needed, then
state the monthly benefit when you retire.
Part II (10 points) - Group
Plan a house mortgage. Monthly payments will be made for 30 years on a
fixed loan rate of 6%. Assume that you make a 20% downpayment.
- Find a house you would like to purchase that costs between $80,000 and
$200,000. Include the address and cost of the home in your project. You can
find homes in the newspaper or online at http://www.realtor.com/decaturil/
- How much is the down payment?
- Compute the monthly payment needed to finance the balance of the
house.
- How much will money will you pay to repay the loan?
- How much interest will you pay?
- It is now ten years later and you have made regular payments on the
house.
- Determine how much money is still owed on the house after 10 years.
- The house is now worth 8% more than what you paid for it. How much is
the house worth?
- How much equity do you have in the house?
- Going back to when you took out the loan, assume that you pay an extra
$250 a month.
- How long will it take to pay off the loan?
- How much will you repay
- How much interest will you pay?
Project 2, Chapter 4
Part I (10 points)
Solve the following matrix equations for X if possible. If it canot be
solved, write "not possible". Assume capital letters represent
matrices.
- AX = B
- AX + BX = C
- XA + XB = C
- AX - X = B
- AX - 3X = B
- XA - 3X = B
- AX + B = CX + D
- X = MX + D
- AXA = B
- AX + XA = B
Part II - The Abilene Network (10 points)
Abilene is a nationwide, high speed, Internet Protocol (IP), research and
education network created by collaboration among Qwest®, Cisco®,
Nortel Networks®, Indiana University and Internet2®. Abilene runs on
over 10,000 miles of the Qwest nationwide Synchronous Optical Network
(SONET) backbone, and Qwest provides facilities and engineering support for
the Abilene Internet Protocol (IP) infrastructure. The contributions of
Qwest and these dedicated Corporate Partners have resulted in the creation
and successful operation of a backbone network with an estimated value of
approximately $500 million.
The predominant Internet2 backbone network, Abilene, is utilized by
leading universities in almost all fifty states, including Alaska and
Hawaii. Nearly 200 U.S. universities take advantage of Abilene to
collaborate on such diverse advanced applications as tele-immersion, virtual
laboratories, distance learning, distributed performing arts, tele-medicine
and digital libraries.
There is a map of the Abilene network at http://abilene.internet2.edu/images/abilene-current.gif.
I have created a blank incidence matrix that
you may wish to print an use to make this easier for you. It requires Adobe
Acrobat Reader to view.
When I write "hop" or "network segment", I mean a
trip between two cities.
- Create an incidence matrix for the Abilene network. List the cities in
alphabetical order.
- What is the maximum number of hops a packet might travel before reaching
its destination? (Hint: find A + A2 + A3 + ... until
every non-diagonal element is greater than zero). Write down this
matrix.
- Part of the design of a good network is redundancy. If any one site
loses connectivity, the rest of the network must continue to function. If
the site at Kansas City goes down, what is the maximum number of hops a
packet might travel before reaching its destination (assume its destination
isn't Kansas City)? Write down the matrix used to determine this
answer.
Project 3, Chapter 7
Part I - Probabilities (10 points)
Find the probabilities of the following winning poker hands. Assume aces
are high and that five cards are drawn from a standard 52 card deck. Show
work and the probabilities.
- Royal Flush - (Five highest cards from ten through ace in any single
suit)
- Straight Flush - (Five cards of the same suit in numerical order)
- Four of a Kind
- Full House - (Three of one kind of card and two of another)
- Flush - (Five cards of the same suit)
- Straight - (Five cards in sequence but not the same suit)
- Three of a Kind
- Two Pairs
- One Pair
- Not a winning hand
Part II - Decision Theory (10 points)
John and Mitchy run a computer store. They can purchase 10 computers from
Zol and Denny for $1400 each, 30 computers from McGuinn and McGuire for
$1300 each, or 50 computers from Sebastian for $1250 each (they can buy from
more than one dealer, but only one order per dealer). John and Mitchy sell
the computers for $1500 each. Each computer that is left at the end of the
month will be sold in a clearance sale for $900. John and Mitchy estimate a
loss of goodwill of $50 for each customer which comes into the store, but is
unable to purchase a computer. During the month, the customers will either
demand 15, 30, 45, or 60 computers. Assume the probability of 15, 30, 45, or
60 computers is 0.10, 0.15, 0.50, and 0.25 respectively.
- Create a payoff table with the five actions (remember that you can
combine purchases from more than one dealer and some plans don't make any
sense when the demand is considered) and four states of nature (demand)
- Create the opportunistic loss (regret) table.
- For each decision criteria (expected value, maximax, maximin, minimax),
find the payoff or loss for each action and the best action.
Project 4, Chapter 9
Part I (10 points)
Consider the following two-person zero-sum game.
| |
Cereal |
Dairy |
Meat |
Snacks |
| Baking |
-3 |
1 |
-5 |
4 |
| Fruits |
2 |
-1 |
-2 |
3 |
| Pasta |
-1 |
1 |
3 |
-2 |
| Soda |
3 |
4 |
-1 |
2 |
The row player is "Rick's Ready Mart" and the column player is
"Corissa's Country Market".
Rick and Corissa own the only two grocery stores in town so that a sale
for Rick is a loss for Corissa and vice versa. Each week, they each run a
special on exactly one type of food in an effort to draw business into their
store. The matrix showing the choices and the gain in sales for Rick's store
are shown.
Answer the following questions.
- If Rick and Corissa each randomly select a food type to put on sale,
what are the strategies and what is the value of the game for Rick?
- What are the optimal strategies for Rick and Corissa? What is the value
of the game for Rick under that those strategies?
- Find the expected payoff values for each of Rick's actions if Corissa
plays her optimal strategies. Find the expected loss values for each of
Corissa's actions if Rick plays his optimal strategies.
- Rick finds out that Corissa is going to spin the spinner from the game
Life (10 slots) and place Cereal on sale if a 1 shows up, Dairy on sale if a
2 or 3 shows up, Meat on sale if a 4, 5, or 6 shows up, and Snacks on sale
if a 7, 8, 9, or 10 shows up.
- What is the expected value of each action for Rick?
- What should Rick's a priori strategy be using the expected value
criterion?
- What should Corissa's strategy really be (not what she said) if the
intent was to trick Rick into playing a particular strategy?
Part II (10 points)
- Create a 4 by 4 non-strictly determined game matrix with no recessive
rows or columns.
- Turn the matrix into a story problem. The matrix can be given as a
matrix, but come up with choices for the row and column players to make it
an interesting problem.
- Solve the game using the calculator.
Project 5, Chapter 10
Part I - Peg Moving (10 points)
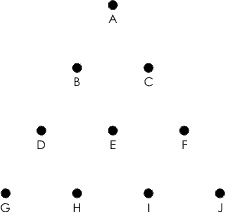 A game is played by placing a peg into one of ten holes arranged
as shown in the figure. The peg is then randomly moved to one of the
adjacent holes (as an example, F is adjacent to C, E, I, and J) until one of
the vertices (A, G, or J) is reached. A worksheet has been created to help you setup the
problem.
A game is played by placing a peg into one of ten holes arranged
as shown in the figure. The peg is then randomly moved to one of the
adjacent holes (as an example, F is adjacent to C, E, I, and J) until one of
the vertices (A, G, or J) is reached. A worksheet has been created to help you setup the
problem.
- Create a transition matrix.
- Find the fundamental matrix F.
- If the game is begun by placing the peg into hole E, how many moves can
be expected to be made before the game is over?
- What is the probability of ending up in hole A if the peg is placed into
hole F to begin with?
Part II - Craps (10 points)
Consider the dice game of craps as an absorbing Markov chain. The rules
of craps are as follow: A pair of dice are rolled. If the sum on the first
roll is a 7 or an 11, you win immediately and the game is over. If the sum
on the first roll is a 2, 3, or 12, you lose immediately and the game is
over. If the sum on the first roll is a 4, 5, 6, 8, 9, or 10, that sum
becomes the "point" and you continue rolling the dice until you
roll your point again and win or you roll a 7 and lose.
A worksheet that can be completed is
available in PDF format. If you complete the last two pages of the
worksheet, then you have answered all the questions below.
- Write a 1×3 matrix indicating the probabilities of winning,
losing, or making a point on the first roll of the dice.
- Find the expected number of rolls before winning or losing and the
probability of winning and losing for each of the point values.
- Find the overall probability of winning and losing a game of craps. Note
that the probabilities of winning and losing for the individual point values
are conditional probabilities ... they are dependent upon rolling that
particular point value on the first roll, so use the general multiplication
rule.
- Find the expected number of rolls for a game of craps. To find the
expected number of rolls for a point (since they're different depending on
the point value), find the expected value of the number of rolls when
weighted with the probability of rolling that point. Be sure and add one to
the number of rolls to include the first roll of the dice.
 A game is played by placing a peg into one of ten holes arranged
as shown in the figure. The peg is then randomly moved to one of the
adjacent holes (as an example, F is adjacent to C, E, I, and J) until one of
the vertices (A, G, or J) is reached. A worksheet has been created to help you setup the
problem.
A game is played by placing a peg into one of ten holes arranged
as shown in the figure. The peg is then randomly moved to one of the
adjacent holes (as an example, F is adjacent to C, E, I, and J) until one of
the vertices (A, G, or J) is reached. A worksheet has been created to help you setup the
problem.