Math 121 - Exam 1 Study Guide

1. Use the table of values to evaluate the combination and composition of functions. Six parts. Look at problem 1.3.47 and review exercise 1.11.
2. A sketch of a function is given. Use that graph to sketch the given transformations. Look at problems 1.3.1-4.
3. Give the exact value of the trigonometric expressions. Five parts. Look at problems 13-14 in appendix A.
4. Given the value of one trigonometric function and the quadrant the angle lies in, find the values of the other five trigonometric functions. Look at problems 15-16 in appendix A.
5. Find all the values of θ in radians that satisfy the given equation. Look at problems 20-27 in appendix A.
6. Find the limit numerically. Look at problems 2.1.13-16.
7. Given the values of two trigonometric functions (example: cos α and sin β), find the exact values of other trigonometric expressions involving α and β. You will need to know many of the formulas from appendix A. α and β are acute angles. Eleven parts. See below for some examples.
8. Given the sketch of a function, find the limits. Also find the value of the function at certain points and determine if the function is continuous at those points. Thirteen parts. Look at problems 2.1.1-6
9. Given the limits of three functions, find combinations of the limits. Five parts. Look at problem 2.2.1, 2.3.5
10. Use the definition of a limit to prove a limit. Look at problems 2.4.21-26, 29-34
11. Find the indicated limits. Six parts. Look at problems 2.2.3-30
12. Find the indicated infinite limits. Three parts. Look at problems 2.3.7-28, 33-36
13. Find the indicated limits involving trigonometric functions. Four parts. Look at problems 2.6.11-32
14. Find the points of discontinuity, if any, and determine whether the discontinuities are removable. Two parts. Look at problems 2.5.11-22, 29-30

Notes

• Most problems are similar to examples we've worked out in class.
• Problems from the book may be similar to the problems on the test, but you should not expect the questions on the test to be identical to those in the book.
• In many cases, the instructions will say to find the limit using algebraic techniques and show any necessary work. Going to the calculator and plugging in values approaching the number is not an algebraic technique. If there is any doubt about whether or not work should be shown, then show it. You may not receive full credit on some of the more difficult problems if you just have an answer. You may check yourself using numeric techniques, but be sure to show work if you do that so I don't think that's how you found the answer.

Examples for #7

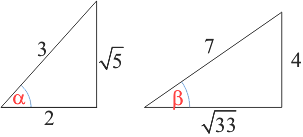Let cos α = 2/3 and sin β = 4/7. Probably the best way to tackle this is to draw two right triangles -- one where the cos α = 2/3 and one where sin β = 4/7. Then use the Pythagorean relationship to find the missing side.

In triangle involving α, the length of the adjacent leg is 2 and the length of the hypotenuse is 3. That makes the length of the opposite leg √5.

In triangle involving β, the length of the opposite leg is 4 and the length of the hypotenuse is 7. That makes the length of the adjacent leg √33.

1. Find sin α. From the triangle involving α, the sin α = √5 / 3.
2. Find cos (π - α). π - α is in the second quadrant where the cosine is negative. So, cos (π - α) = - cos α = - 2/3.
3. Find tan (α+β). Since tan (α+β) = [ tan α + tan β] / [ 1 - tan α tan β ], we need to know tan α and tan β.
   From the triangles you drew, you can see that tan α = √5 / 2 and tan β = 4 / √33.
   Then tan (α+β) = [ √5 / 2 + 4 / √33 ] / [ 1 - (√5 / 2) (4 / √33) ].
   Now multiply top and bottom by the LCD = 2√33 to get [ √165 + 8 ] / [ 2√33 - 4√5 ].

Point values per problem

Go to Math 121 homepage

Last updated: June 17, 2008 10:42 PM