Math 121 - Exam 1 Study Guide
- Factor the expression completely. Three parts.
- Use the table of values to evaluate the expressions. Five parts.
- Find the limit numerically. Look at problems 2.1.13-16.
- Give the exact value of the trigonometric expressions. Six parts. Look at problems 13-14 in appendix A.
- Find all the values of x in radians that satisfy the given equation.
Two parts. Look at problems 20-27 in appendix A.
- Given the values of two trigonometric functions (example: cos α and sin β), find the exact values of other trigonometric expressions involving α and β. You will need to know many of the formulas from appendix A. α and β are acute angles. Fourteen parts. See below for some examples.
- Given the sketch of a function, find the limits. Also find the value of the
function at certain points and determine if the function is continuous at
those points. Fifteen parts. Look at problems 2.1.1-6
- Given the limits of three functions, find combinations of the limits. Four parts. Look at problem 2.2.1, 2.3.5
- Use the definition of a limit to prove a limit. Look at problems 2.4.21-26, 29-34
- Find the indicated limits. Eight parts. These may be done without showing work.
- Find the indicated limits involving trigonometric functions. Show work. Six parts. Look at problems 2.6.11-32
- Find the indicated limits. Six parts. Look at problems 2.2.3-30 and 2.3.7-28, 33-36
- Find the points of discontinuity, if any, and determine whether the discontinuities
are removable. Two parts. Look at problems 2.5.11-22, 29-30
Notes
- Most problems are similar to examples we've worked
out in class.
- Problems from the book may be similar to the problems on the test, but you should not expect the questions on the test to be identical to those in the book.
- In many cases, the instructions will say to find the limit using algebraic techniques and show work. Going to the calculator and plugging in values approaching the number is not an algebraic technique. If there is any doubt about whether or not work should be shown, then show it. You may not receive full credit on some of the more difficult problems if you just have an answer. You may check yourself using numeric techniques, but be sure to show work if you do that so I don't think that's how you found the answer.
Examples for #6
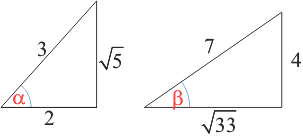Let cos α = 2/3 and sin β = 4/7. Probably the best way to tackle this is to draw two right triangles -- one where the cos α = 2/3 and one where sin β = 4/7. Then use the Pythagorean relationship to find the missing side.
In triangle involving α, the length of the adjacent leg is 2 and the length of the hypotenuse is 3. That makes the length of the opposite leg √5.
In triangle involving β, the length of the opposite leg is 4 and the length of the hypotenuse is 7. That makes the length of the adjacent leg √33.
- Find sin α. From the triangle involving α, the sin α = √5 / 3.
- Find cos (π - α). π - α is in the second quadrant where the cosine is negative. So, cos (π - α) = - cos α = - 2/3.
- Find tan (α+β). Since tan (α+β) = [ tan α + tan β] / [ 1 - tan α tan β ], we need to know tan α and tan β.
From the triangles you drew, you can see that tan α = √5 / 2 and tan β = 4 / √33.
Then tan (α+β) = [ √5 / 2 + 4 / √33 ] / [ 1 - (√5 / 2) (4 / √33) ].
Now multiply top and bottom by the LCD = 2√33 to get [ √165 + 8 ] / [ 2√33 - 4√5 ].
Point values per problem
| # |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
Total |
| Pts |
9 |
10 |
4 |
12 |
6 |
14 |
15 |
8 |
6 |
24 |
18 |
18 |
6 |
150 |