Minitab Notes for Activity 2

In these instructions, I refer to different units such as PSI, Torrs, or Pascals. For your activity, I have removed the unit conversion to shorten up the activity, but haven't had time to go through and rework all the examples. Just use the variables you have.

Creating the Worksheet

The worksheet will be provided to you by the instructor. That is so that you won't know whose blood pressure and pulse rate is whose. Although gender and age may be related to blood pressure and pulse rate, we're not collecting that information for this project. If this were a more clinical study, we would collect and analyze that data and more.

The variables recorded are called systolic, diastolic, and pulse.

  1. Choose File / Open Worksheet (make sure it's open worksheet and and not open project)
  2. Move through the file system to R:
  3. Change to your section number
  4. Change to the act2 folder
  5. Open the worksheet called bp.mtw
  6. Choose File / Save Project As
  7. Type a name that is unique to your group
  8. Click OK

From now on, when you need to work with the project, open the one for your group.

Generate a Scatterplot (Question 4)

Scatterplot of diastolic pressure in Pa vs systolic pressure in psiThis question wants you to generate a scatterplot and try to determine the value of the correlation coefficient based on the scatterplot alone.

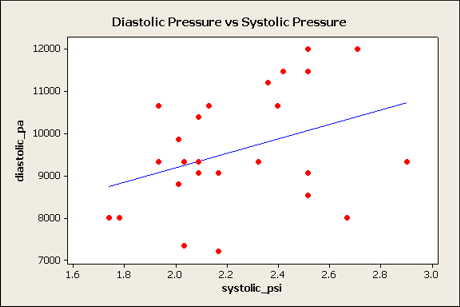
This example assumes that my predictor (x) variable is systolic blood pressure in psi (systolic_psi) and the response (y) variable is diastolic blood pressure in Pascals (diastolic_pa). Be sure you use your variables!

  1. Choose Graph / Scatterplot
  2. Choose With Regression
  3. For the Y variable, double click on your response variable (mine is disastolic_pa)
  4. For the X variable, double click on your predictor variable (mine is systolic_psi)
  5. (Optional) Add a title by clicking Labels
  6. Click OK

Now make a guess as to what you think the correlation coefficient would be. For my data, there appears to be a very slight positive correlation, but it's not very good at all. I would guess about r = 0.1.

Fitted Line Plot of Standardized Variables (Question 5)

My variables are diastolic_pa and systolic_psi. You should use whichever variables you're working with instead of the ones in my example. The units aren't necessary on the standardized variables because z-scores don't have units.

Standardize the variables

  1. Create two new variables with a z_ prefix.
    1. Label one empty column as z_systolic
    2. Label another empty column as z_diastolic
  2. Choose Calc / Standardize
  3. Use systolic_pa and diastolic_pa as the input columns
  4. Store the results in z_systolic and z_diastolic
  5. Click OK

Note that you do not need to include the units with the standardized variables because there are no units. The standardized variables are found by subtracting the mean and dividing by the standard deviation. For example, if a diastolic blood pressure was 80 torr and it came from a sample with a mean of 86 torr with a standard deviation of 12 torr, then the standardized value would be (80 torr - 86 torr) / (12 torr) = (-6 torr) / (12 torr) = -0.5 (the units divide out, so there are no units).

Fitted Line Plot

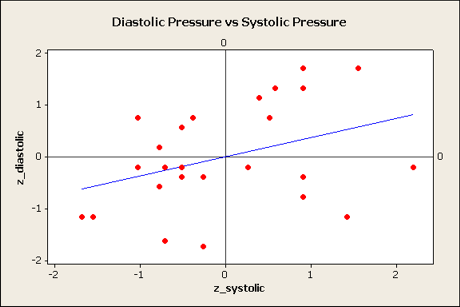Fitted line plot of standardized variablesRepeat the steps above, but use the z_ variables instead of the unitized variables. You will notice that the graphs for the original and the standardized variables look the same, only the scale has changed.

  1. Choose Graph / Scatterplot
  2. Choose With Regression
  3. For the Y variable, double click on your response variable (mine is z_disastolic)
  4. For the X variable, double click on your predictor variable (mine is z_systolic)
  5. (Optional) Add a title by clicking Labels
  6. Click on Scale
    1. Click on the Reference Lines tab
    2. Add a reference line at 0 for both the Y and the X positions. This will add a set of axes that will help you determine the slope
  7. Click OK

The important thing to realize is that the correlation coefficient, r, is the slope of the standardized regression line, not the one for the original data.

Estimating r by the slope of the line

Find the coordinates of a point on the line. By point, I don't mean data points (the dots), I just mean a point somewhere on the line. You may be lucky enough to have a data point on the line that you could figure out the coordinates for, but probably not.

If I take a straightedge and go straight up from the 1 on the x-axis to the line, it looks like the y-value is about 0.4. The best fit line for a standardized plot will always pass through the origin, so now I have two points. From the point (0,0) to the point (1,0.4), my rise is 0.4 and my run is 1. Since slope is rise over run, my slope and correlation coefficient would be about 0.4/1 = 0.4.

Summarizing the Data (Question 6)

I'm going to describe my predictor variable of systolic_psi and my response variable of diastolic_pa. Be sure you use your variables instead of mine.

  1. Choose Stat / Basic Statistics / Display Descriptive Statistics
  2. Double click on your two variables (mine are systolic_psi and diastolic_pa)
  3. Click OK

You should get some output that looks like this.

Variable       N  N*    Mean  SE Mean   StDev  Minimum      Q1  Median      Q3
systolic_psi  25   0  2.2407   0.0599  0.2993   1.7403  2.0207  2.1657  2.5138
diastolic_pa  25   0    9605      279    1395     7199    8666    9333   10666

Variable      Maximum
systolic_psi   2.9005
diastolic_pa    11999

Copy the sample size, mean, and standard deviation onto your activity sheet.

Finding Correlation (Question 7)

I'm going to find the correlation between my variables of systolic_psi and diastolic_pa. Be sure you use your variables instead of mine.

  1. Choose Stat / Basic Statistics / Correlation
  2. Double click on the predictor variable (systolic_psi) and then double click on the response variable (diastolic_pa).
  3. Click OK

You will get something that looks like this. The first number is the correlation coefficient. The second number is the p-value.

Pearson correlation of systolic_psi and diastolic_pa = 0.369
P-Value = 0.069

Now, repeat these steps, but put the response variable first and the predictor variable second.

Regression (Question 9)

I'm going to describe my predictor variable of systolic_psi and my response variable of diastolic_pa. Be sure you use your variables instead of mine

  1. Choose Stat / Regression / Regression
  2. Use your response variable for the response variable (mine is diastolic_pa)
  3. Use your predictor variable for the predictor variables (mine is systolic_psi). Even though there is room for more than one predictor variable, we're not going to have more than one until the end of the book when we talk about multiple regression.
  4. Click OK

You will get a lot of information. The part we want for question 9 is just the first line of all that.

The regression equation is
diastolic_pa = 5749 + 1721 systolic_psi

ANOVA table (Question 10)

There will be an "Analysis of Variance" table that is generated as part of the regression output from question 10. It looks something like this.

Analysis of Variance
Source            DF          SS          MS         F        P
Regression         1     6365998     6365998      3.63    0.069
Residual Error    23    40363404     1754931
Total             24    46729402

Copy down the numbers onto your activity sheet. Note that on the activity sheet, the "residual error" is abbreviated as "residual".

Use the explanation on your activity sheet about the ANOVA table to answer question 11.

Go to Math 113 Activities page.

Go to Math 113 homepage

Last updated June 8, 2004 8:34 AM