Project 3: Inverses

Instructions

Use Winplot and Google Docs to create a document with three problems on it. You may be able to locate similar problems in the book, but these problems should be your original creations.

Problem 1: Graphing Inverses

1. Create a one-to-one function and pick a point on it where the derivative is not zero.
2. Find the instantaneous rate of change at the point.
3. Find the equation of the tangent line at that point.
4. Find the point on the inverse that corresponds to your original point.
5. Find the derivative of the inverse at that corresponding point.
6. Find the equation of the tangent line to the inverse at that corresponding point.
7. Create a graph that has: both functions (to graph the inverse, you can use Winplot to reflect the curve or graph it implicitly), the line y=x, both points, and both tangent lines.

Example Graph

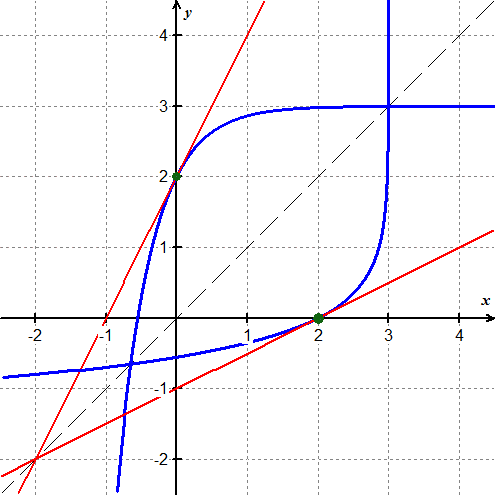
You still need the answers to the other parts, but this is an example of what a graph might look like.

Problem 2: Derivatives of Trigonometric Functions

Create 3 graphs, one for each pair of inverse trigonometric functions. Graph the inverse trigonometric function and its derivative. Then repeat the process for its cofunction. Develope and use a color scheme to illustrate that the inverse functions are symmetric about the line \( y=\frac{\pi}{4} \)and the derivatives of the inverse cofunctions are opposites of each other.

Problem 3: Curve Fitting

Create problems that require fitting a curve to the given points. Provide a worked out solution with graph (to verify the solution) to the problem.

• Fit the function \( f(x) = A \ln x + B \) to two points (positive x values only)
• Fit the function \( f(x) = A e^{kx} + B \) to a y-intercept, a horizontal asymptote, and a second point.

Example Problem

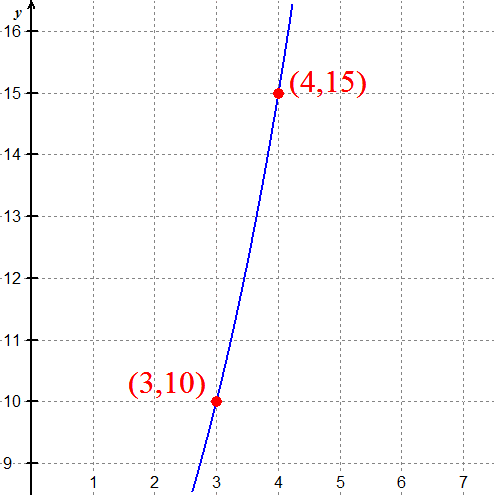
Find constants A and k so that the function \( f(x) = Ae^{kx} \) passes through (3,10), and (4,15).

Example Solution

You may find it easier to work the solution out on paper, take a picture with your cell phone, and upload that into Google Docs than to use the equation editor to type all this. Also note that I worked out the exact answers, most people go with decimal approximations. If you do this, wait until the end to round.

Substituting the points into the function gives: \( 10 = Ae^{3k} \) and \( 15 = Ae^{4k} \)

Divide those two equations to get \( \frac {15}{10} = \frac{Ae^{4k}}{Ae^{3k}} \), which simplifies to be \( \frac{3}{2} = e^k \).

Taking the natural logarithm of both sides gives \( k = \ln \frac 3 2 \).

Plugging that back into the first equation gives \( 10 = Ae^{3 \ln 3/2} = Ae^{(\ln 3/2)^3} = A \left ( \frac 3 2 \right )^3 \)

Solving for A yields \( A = 10 \left ( \frac 2 3 \right )^3 = \frac {80}{27} \).

The function is \( f(x) = \frac {80}{27} e^{x \ln 3/2} \).

You could also use decimal approximations to get \( f(x) = 2.96 e^{0.405 x} \).

Notes

• Add your names at the top of the document under the title.
• Include instructions with each of the problems; don’t just create a graph or describe the graph.

Submitting the Assignment

Once you are done with the assignment, share it with the instructor. Only one person per group needs to submit the assignment, just make sure your names are all in the document itself.

1. Click the blue "Share" button in Google Docs
2. In the "Invite People" box, put in james@richland.edu
3. Change the permissions from "Can edit" to "Can comment"
4. Leave the box checked to notify people via email (This is important or I won't know that you've turned it in).
5. Click on the "Add message" box and let me know what you're sending and the names of the people in your group.
6. Click "Send"

Help

• Winplot help
• Google Docs help