Use Winplot and Google Docs to create a document with three problems on it. You may be able to locate similar problems in the book, but these problems should be your original creations.
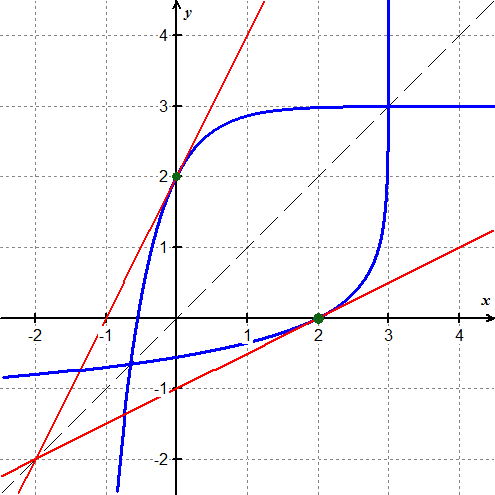
You still need the answers to the other parts, but this is an example of what a graph might look like.

Create 3 graphs, one for each pair of inverse trigonometric functions. Graph the inverse trigonometric function and its derivative. Then repeat the process for its cofunction. Develope and use a color scheme to illustrate that the inverse functions are symmetric about the line \( y=\frac{\pi}{4} \)and the derivatives of the inverse cofunctions are opposites of each other.
Create problems that require fitting a curve to the given points. Provide a worked out solution with graph (to verify the solution) to the problem.
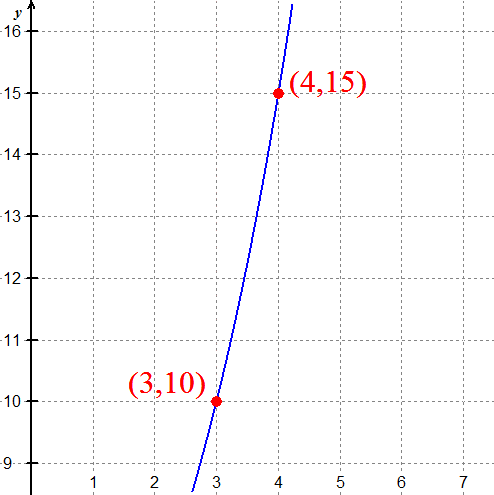
Find constants A and k so that the function \( f(x) = Ae^{kx} \) passes through (3,10), and (4,15).
You may find it easier to work the solution out on paper, take a picture with your cell phone, and upload that into Google Docs than to use the equation editor to type all this. Also note that I worked out the exact answers, most people go with decimal approximations. If you do this, wait until the end to round.
Substituting the points into the function gives: \( 10 = Ae^{3k} \) and \( 15 = Ae^{4k} \)
Divide those two equations to get \( \frac {15}{10} = \frac{Ae^{4k}}{Ae^{3k}} \), which simplifies to be \( \frac{3}{2} = e^k \).
Taking the natural logarithm of both sides gives \( k = \ln \frac 3 2 \).
Plugging that back into the first equation gives \( 10 = Ae^{3 \ln 3/2} = Ae^{(\ln 3/2)^3} = A \left ( \frac 3 2 \right )^3 \)
Solving for A yields \( A = 10 \left ( \frac 2 3 \right )^3 = \frac {80}{27} \).
The function is \( f(x) = \frac {80}{27} e^{x \ln 3/2} \).
You could also use decimal approximations to get \( f(x) = 2.96 e^{0.405 x} \).
Once you are done with the assignment, share it with the instructor. Only one person per group needs to submit the assignment, just make sure your names are all in the document itself.