
Use Winplot and Google Docs to create a document with three problems on it. You may be able to locate similar problems in the book, but these problems should be your original creations.
Use Winplot to create a graph that has a function and its first and second derivative graphed all on the same coordinate system. Use some scheme (color or thickness) to identify the different curves. Ask the user to identify which function is g(x), which is g'(x), and which is g''(x).
Repeat this so that you have 4 graphs all together. Mix up the graphs so there is a good selection of function types. Do not use the same color scheme for each graph.
Provide an answer key at the end of the project.
Identify which function is the graph of y=g(x), y=g'(x), and y=g''(x).

The red curve is g, the blue curve is g', and the green curve is g''.
You need to do this portion on paper and pencil. Either scan the document (or take a picture with your cell phone) and then upload it into the Google document. Do not shrink the size; make sure it's big enough to read everything.
Find the digit sum of the birthdates (month and day only) of the people in your group to decide which function you will use. Example: If birthdays are 1/25 and 3/18, then 1+2+5+3+1+8 = 20, then 2+0 = 2, so the digit sum is 2. You would use function #2.
Take the function determined using the digit sum method and go through the 8 step process in the textbook in section 4.4.Sketch the graph by hand on paper.
After you have done all the work by hand, use Winplot to make the graph. Be sure to change the settings on the graph so that the important features of the graph are shown.
Note that some of the zeros may be difficult to find by hand; you can use Maxima and its solve() or find_root() commands to assist. After typing the command, you either press shift-enter or the enter on the numeric keypad to execute the command.
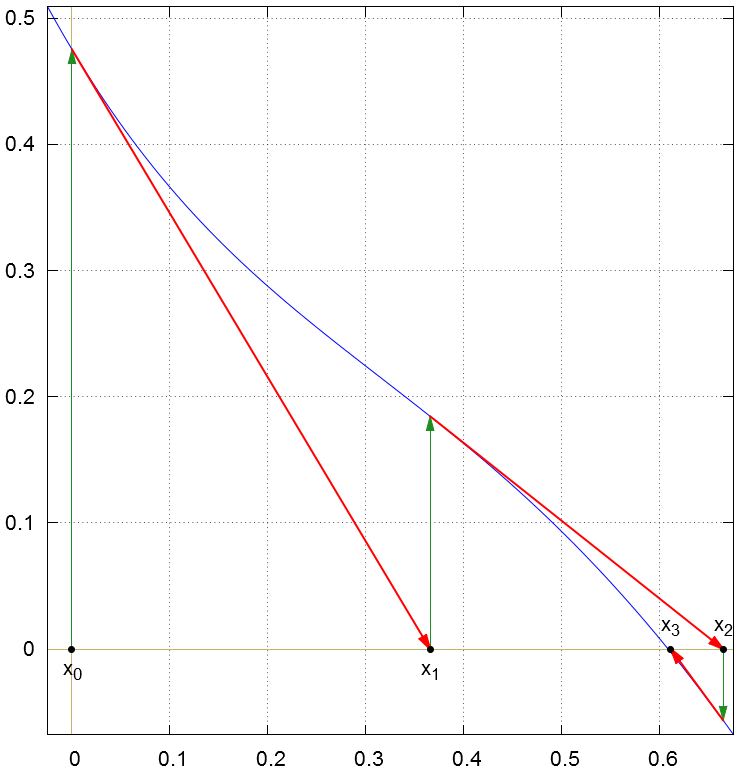
Create a function with an x-intercept and then apply Newton's method to find that x-intercept. Continue to iterate until you get the same x-value twice in a row.
Create a graph that will illustrate Newton's method for that problem with for at least two iterations.
The function \(f(x) = (x-1)(x-3)(1-0.5e^{0.3-x^2})-0.5\) has a zero between \(x=-1\) and \(x=2\). Use Newton's Method to find it.
We'll start off with an initial guess of \(x_0 = 0\).
| \(n\) | \(x_n\) | \(y_n\) | \(y_n'\) |
|---|---|---|---|
| 0 | 0 | 0.475211789 | -1.300282385 |
| 1 | 0.365468143 | 0.184488271 | -0.61695879 |
| 2 | 0.664496659 | -0.056502485 | -1.059827831 |
| 3 | 0.611183769 | -0.002665516 | -0.959869638 |
| 4 | 0.608406813 | -7.18906E-06 | -0.954693235 |
| 5 | 0.608399283 | -5.3E-11 | -0.954679209 |
| 6 | 0.608399282 | 0 | -0.954679209 |
| 7 | 0.608399282 |
The solution is x = 0.608399282.
Once you are done with the assignment, share it with the instructor. Only one person per group needs to submit the assignment, just make sure your names are all in the document itself.