 When
the major axis is horizontal, the foci are at (-c,0) and at (0,c).
When
the major axis is horizontal, the foci are at (-c,0) and at (0,c).An ellipse is the set of all points in a plane such that the sum of the distances from two fixed points (foci) is constant.
 When
the major axis is horizontal, the foci are at (-c,0) and at (0,c).
When
the major axis is horizontal, the foci are at (-c,0) and at (0,c).
Let d1 be the distance from the focus at (-c,0) to the point at (x,y). Since this is the distance between two points, we'll need to use the distance formula.
![]()
Similarly, d2 will involve the distance formula and will be the distance from the focus at the (c,0) to the point at (x,y).
![]()
We can use the fact that the vertices are on the ellipse to find out what the sum of the distances is.
If we take the vertex on the right, then d1 = a + c and d2 = a - c.
d1 + d2 = ( a + c )+ ( a - c ) = 2a
Therefore, the constant is 2a and d1 + d2 = 2a for every point on an ellipse.
Now that we know what the sum of the distances is, we can set about finding the equation of the ellipse.
We start with d1 + d2 = 2a and substitute the formulas for d1 and d2.
![]()
We want to get rid of the radicals, so we'll move one term to the other side and then square both sides of the equation.
![]()
![]()
Let's multiply out the squared terms
![]()
If we move everything except for the square root term to the left side, a lot of this will cancel out and we'll get
![]()
Let's divide everything by -4 to get
![]()
Square both sides to get rid of the radical
![]()
Expand the (x-c)2 on the right hand side
![]()
Distribute the a2 on the right side
![]()
Move all the variable terms to one side and the constants to the other.
![]()
Factor and x2 out of the first two terms on the left and an a2 out of the right side.
![]()
Notice how there is an a2 - c2 on both sides. Let's define b2 = a2 - c2 and make the substitution into the equation.
![]()
Finally, divide everything by a2b2 so the right side is 1.
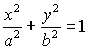
That gives us the standard form for an ellipse with a horizontal major axis and it also gives us the Pythagorean relationship a2 = b2+ c2.
Return to notes on conic sections.