8.1 - Conics

The conics get their name from the fact that they can be formed by passing a plane through a double-napped cone. There are four conic sections, and three degenerate cases, however, in this class we're going to look at five degenerate cases that can be formed from the general second degree equation.

The general form of a second degree equation is given by Ax² + Bxy + Cy² + Dx + Ey + F = 0

Determining Conic Sections by Inspection

To determine the conic section by inspection, complete any squares that are necessary, so that the variables are on one side and the constant is on the right hand side. Any squared variable below could be replaced by a quantity. That is, instead of x² + y² = 1, it might be (x-2)² + y² = 1

Circle: x² + y² = 1; Both squared terms are present, both are positive, both have the same coefficient. The right hand side is positive. If the right hand side is zero, it is a point. If the right hand side is negative, then there is no graph.
Ellipse: 3x² + 4y² = 1; Both squared terms are present, both are positive, but they have different coefficients. The right hand side must be positive. If the right hand side is zero, it is a point. If the right hand side is negative, then there is no graph.
Hyperbola: x² - y² = 1; Both squared terms are present, but one is positive and the other is negative. The coefficients may or may not be the same, it doesn't matter. The right hand side isn't zero. If the right hand side is zero, then it's intersecting lines.
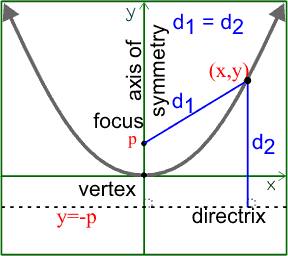
Parabola: x² + y = 1; Both variables are present, but one is squared and the other is linear.
Line: x + y = 1; Neither variable is squared.
Point: x² + y² = 0; A circle (or ellipse) with the right hand side being zero.
No Graph: x² + y² = -1; A circle (or ellipse) with the right hand side being negative.
Intersecting Lines: x² - y² = 0; A hyperbola with the right hand side equal to zero.
Parallel Lines: x² = 1; One variable is squared and the other variable is missing. The right hand side must be positive. If the right hand side is zero, then it is a line (x² = 0 so x = 0) and if the right hand side is negative (x² = -1), then there is no graph.

Parabola

A parabola is "the set of all points in a plane equidistant from a fixed point (focus) and a fixed line (directrix)".

The distances to any point (x,y) on the parabola from the focus (0,p) and the directrix y=-p, are equal to each other. This can be used to develop the equation of a parabola.

If you take the definition of a parabola and work out the algebra, you can develop the equation of a parabola. You can click on the link if you'd like to see the development, but the short version is that the standard form is x² = 4py.

The starting point is the vertex at (h,k)
There is an axis of symmetry that contains the focus and the vertex and is perpendicular to the directrix.
Move p units along the axis of symmetry from the vertex to the focus.
Move -p units along the axis of symmetry from the vertex to the directrix (which is a line).
The focus is within the curve.

The parabola has the property that any signal (light, sound, etc) entering the parabola parallel to the axis of symmetry will be reflected through the focus (this is why satellite dishes and those parabolic antennas that the detectives use to eavesdrop on conversations work). Also, any signal originating at the focus will be reflected out parallel to the axis of symmetry (this is why flashlights work).

Circle

A circle is "the set of all points in a plane equidistant from a fixed point (center)".

The standard form for a circle, with center at the origin is x² + y² = r², where r is the radius of the circle.

Ellipse

An ellipse is "the set of all points in a plane such that the sum of the distances from two fixed points (foci) is constant".

The sum of the distances to any point on the ellipse (x,y) from the two foci (c,0) and (-c,0) is a constant. That constant will be 2a.

If we let d₁ and d₂ bet the distances from the foci to the point, then d₁ + d₂ = 2a.

You can use that definition to derive the equation of an ellipse, but I'll give you the short form below.

The ellipse is a stretched circle. Begin with the unit circle (circle with a radius of 1) centered at the origin. Stretch the vertex from x=1 to x=a and the point y=1 to y=b. What you have done is multiplied every x by a and multiplied every y by b.

In translation form, you represent that by x divided by a and y divided by b. So, the equation of the circle changes from x² + y² = 1 to (x/a)² + (y/b)² = 1 and that is the standard equation for an ellipse centered at the origin.

The center is the starting point at (h,k).
The major axis contains the foci and the vertices.
Major axis length = 2a. This is also the constant that the sum of the distances must add to be.
Minor axis length = 2b.
Distance between foci = 2c.
The foci are within the curve.
Since the vertices are the farthest away from the center, a is the largest of the three lengths, and the Pythagorean relationship is: a² = b² + c².

Hyperbola

A hyperbola is "the set of all points in a plane such that the difference of the distances from two fixed points (foci) is constant".

The difference of the distances to any point on the hyperbola (x,y) from the two foci (c,0) and (-c,0) is a constant. That constant will be 2a.

If we let d₁ and d₂ bet the distances from the foci to the point, then | d₁ - d₂ | = 2a.

The absolute value is around the difference so that it is always positive.

You can use that definition to derive the equation of a hyperbola, but I'll give you the short form below.

The only difference in the definition of a hyperbola and that of an ellipse is that the hyperbola is the difference of the distances from the foci that is constant and the ellipse is the sum of the distances from the foci that is constant.

Instead of the equation being (x/a)² + (y/b)² = 1, the equation is (x/a)² - (y/b)² = 1.

The graphs, however, are very different.

The center is the starting point at (h,k).
The Transverse axis contains the foci and the vertices.
Transverse axis length = 2a. This is also the constant that the difference of the distances must be.
Conjugate axis length = 2b.
Distance between foci = 2c.
The foci are within the curve.
Since the foci are the farthest away from the center, c is the largest of the three lengths, and the Pythagorean relationship is: a² + b² = c².

Standard Forms

The table below summarizes the standard forms for the three main conic sections based on the direction of the main axis. For a parabola, the axis is the "axis of symmetry" and divides the parabola in half. For the ellipse, it's called the "major axis" and is the longer axis. For the hyperbola, the axis is the "transverse axis" and goes between the vertices.

	Horizontal Axis	Vertical Axis
Parbola
Ellipse
Hyperbola