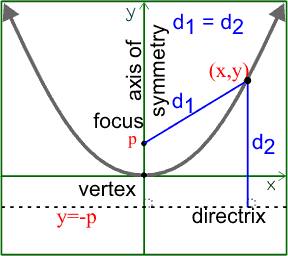
 In its simplest form, the parabola with focal length p has its vertex at the
origin (0,0) and the focus is at the point (0,p). The directrix is the line
y=-p.
In its simplest form, the parabola with focal length p has its vertex at the
origin (0,0) and the focus is at the point (0,p). The directrix is the line
y=-p.A parabola is the set of all points in a plane that are equidistant between a fixed point (focus) and a line (directrix).
 In its simplest form, the parabola with focal length p has its vertex at the
origin (0,0) and the focus is at the point (0,p). The directrix is the line
y=-p.
In its simplest form, the parabola with focal length p has its vertex at the
origin (0,0) and the focus is at the point (0,p). The directrix is the line
y=-p.
Any point (x,y) on the parabola will be the same distance from the focus as it is from the directrix. That is, if d1 is the distance from the focus to the point on the parabola, and d2 is the distance from the directrix to the point on the parabola, then d1=d2.
Since d1 is the distance between two points, (0,p) and (x,y), we need to use the distance formula to find it.
![]()
d2 is the distance between the point (x,y) and a horizontal line y=-p. The x-coordinates will be the same, so the distance between the point and line is the difference in the y-values.
![]()
We earlier said that the parabola is where d1 = d2. Let's set them equal to each other and then square both sides to get rid of the square root.
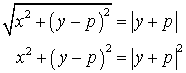
Now, let's expand both sides
![]()
Move everything but the x2 to the right side and simplify. This gives you the standard form for a parabola with vertex at the origin and opening up.
x2 = 4py
Return to notes on conic sections.