Stats: Regression

The idea behind regression is that when there is significant linear correlation, you can use a line to estimate the value of the dependent variable for certain values of the independent variable.

The regression equation should only used

• When there is significant linear correlation. That is, when you reject the null hypothesis that rho=0 in a correlation hypothesis test.
• The value of the independent variable being used in the estimation is close to the original values. That is, you should not use a regression equation obtained using x's between 10 and 20 to estimate y when x is 200.
• The regression equation should not be used with different populations. That is, if x is the height of a male, and y is the weight of a male, then you shouldn't use the regression equation to estimate the weight of a female.
• The regression equation shouldn't be used to forecast values not from that time frame. If data is from the 1960's, it probably isn't valid in the 1990's.

Assuming that you've decided that you can have a regression equation because there is significant linear correlation between the two variables, the equation becomes: y' = ax + b or y' = a + bx (some books use y-hat instead of y-prime). The Bluman text uses the second formula, however, more people are familiar with the notion of y = mx + b, so I will use the first.

a is the slope of the regression line:

b is the y-intercept of the regression line:

The regression line is sometimes called the "line of best fit" or the "best fit line".

Since it "best fits" the data, it makes sense that the line passes through the means.

The regression equation is the line with slope a passing through the point

Another way to write the equation would be

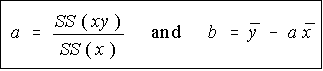apply just a little algebra, and we have the formulas for a and b that we would use (if we were stranded on a desert island without the TI-82) ...

It also turns out that the slope of the regression line can be written as . Since the standard deviations can't be negative, the sign of the slope is determined by the sign of the correlation coefficient. This agrees with the statement made earlier that the slope of the regression line will have the same slope as the correlation coefficient.

TI-82

Luckily, the TI-82 will find these values for us (isn't it a wonderful calculator?). We can also use the TI-82 to plot the regression line on the scatter plot.