Math 160 - Projects
Listed below are the various projects that will be assigned throughout
the semester. These projects take you above and beyond the material covered
in the book or require outside data acquisition.
Each of these projects is worth 20 points and is due two class periods
after the scheduled lecture for the corresponding chapter is finished. Due
dates are noted on the class calendar.
You are encouraged to work in groups of up to three people per project (with the exception of the first part of the first project, which is an individual project). Turn in one project with all group member's names on it.
Plan on reading the section of the book dealing with the matter before we
cover it in class; you will not always have time to finish the project if
you wait until we do.
Some of these projects are very similar to problems that will appear on
your exam. So even though they may not be due until after the exam, it would
be wise for you to work and understand them before the exam.
Project 1, Chapter 3
Part I (10 points) - Individual
Your project is to plan a retirement fund for yourself. To simplify
calculations, assume all transactions - starting of annuity fund,
retirement, and death - occur on your birthday. Assume a nominal interest
rate of 3% has been guaranteed for the remainder of your life. There is a financial planning worksheet to give you an idea of the
format I'm looking for. Feel free to use that paper to write your answers
on.
- Identify the age you will be on your birthday this year.
- Identify the age at which you wish to retire. Identify the number of
years before retirement.
- Identify the age at which you anticipate dying. Identify the number of
years of retirement.
- Identify the monthly payment you anticipate needing during your
retirement.
- Calculate the present value necessary on the date of retirement to
finance your retirement.
- The present value needed to retire is the future value necessary upon
retirement. Calculate the monthly payment needed before retirement to have
enough money to retire.
- Calculate the amount of money in your retirement fund after ten years
assuming you make the regular payments just calculated.
- After the ten years, assume that you receive an inheritance of $20,000
and add it to your retirement fund. If you stop making regular payments, and
just let what money is in the account draw interest, what will the amount be
at the time of retirement?
- Subtract this amount from the future value needed upon retirement and
recompute the monthly payment necessary to obtain the future value. Remember
that ten years have gone by. If no more monthly payments are needed, then
state the monthly benefit when you retire.
Part II (10 points) - Group
Plan a house mortgage. Monthly payments will be made for 30 years on a
fixed loan rate of 6%. Assume that you make a 20% downpayment.
- Find a house you would like to purchase that costs between $80,000 and
$200,000. Include the address and cost of the home in your project. You can
find homes in the newspaper or online at http://www.realtor.com/decaturil/
- How much is the down payment?
- Compute the monthly payment needed to finance the balance of the
house.
- How much will money will you pay to repay the loan?
- How much interest will you pay?
- It is now ten years later and you have made regular payments on the
house.
- Determine how much money is still owed on the house after 10 years.
- How much is the house worth if it is now worth 8% more than what you paid for it?
- How much equity do you have in the house?
- Going back to when you took out the loan, assume that you pay an extra
$250 a month.
- How long will it take to pay off the loan?
- How much will you repay
- How much interest will you pay?
Project 2, Chapter 4
Create a Google Spreadsheet and share it with all members of your group and with the instructor. Have two worksheets, one for each part.
Part I - Dominance Relation (10 points)
Create a dominance relation matrix for the 2013 National League of Major League Baseball. You can do this quickly by using the information at Baseball-Reference.com. Under the "Schedule & Results" for each team, they have an "Opponent" table that lists how many times the team won or lost against the opponent. For example, the 2013 Chicago Cubs information is at http://www.baseball-reference.com/teams/CHC/2013-schedule-scores.shtml. You need to restrict yourself to the National League teams.
In an effort to predict the rankings for the 2014 season, a bookie awards as follows (the overall score is the total of the three scores).
- 15 points for each time the row team directly beats the column team.
- 7 points for each time the row team beats a team who beat the column team.
- 3 points for each time the row team beats a team who beats a team who beat the column team.
- Write a matrix expression that can be used to find the overall score for each team.
- How many points did New York Mets directly receive from the San Francisco Giants?
- How many total points did Chicago Cubs receive from the Cincinnati Reds?
- List the teams and their overall scores.
Part II - Incidence Matrix (10 points)
Cox is a major cable company (just not in Central Illinois). They have a map of their business network at http://ww2.cox.com/wcm/en/business/datasheet/national-ip-backbone-map.pdf
- Create an incidence matrix for the Cox business network (all traffic is bi-directional) between the regional data centers (ignore the local market backbone nodes). List all cities alphabetically.
- Which regional centers are the furthest apart network-wise? That is, which sites require the most segments to get between them? How many hops are needed to connect those cities?
- Part of a good network is building in redundancy. If a regional center goes offline, the traffic needs to be able to get from its source to its destination, although it may take more network segments to do so. Which regional data center, if it were to go offline, would cause the largest number of network segments between any other centers? How many hops are needed to connect those cities? This is basically question 2, except removing one data center at a time.
Project 3, Chapter 8
Part I - Poker Probabilities (5 points)
Find the probabilities of the following winning poker hands. Assume aces
are high and that five cards are drawn from a standard 52 card deck. Show
work and the probabilities.
- Four of a Kind
- Full House - (Three of one kind of card and two of another)
- Three of a Kind
- Two Pairs
- One Pair
Part II - Illinois Lottery (5 points)
Use the information on the Mega Millions and Illinois Lottery websites to answer this part. The rules and the chances of winning are given on the website. The chances of winning are given on the website, so it is important that you show the work necessary to arrive at the answer. Show your work in finding the probabilities that a ticket will win the following prizes. (Hint: Think of the Mega Millions game as a combination of two separate games, each using a hypergeometric distribution).
- Mega Millions game, second prize
- Mega Millions game, third prize
- Mega Millions game, fourth prize
- Lotto, second prize
- Lotto, third prize
Part III - Decision Theory (10 points)
John and Mitchy run a computer store. They can purchase 10 computers from
Zol and Denny for $1400 each, 30 computers from McGuinn and McGuire for
$1300 each, or 50 computers from Sebastian for $1250 each (they can buy from
more than one dealer, but only one order per dealer). John and Mitchy sell
the computers for $1500 each. Each computer that is left at the end of the
month will be sold in a clearance sale for $900. John and Mitchy estimate a
loss of goodwill of $50 for each customer which comes into the store, but is
unable to purchase a computer. During the month, the customers will either
demand 15, 30, 45, or 60 computers. Assume the probability of 15, 30, 45, or
60 computers is 0.10, 0.15, 0.50, and 0.25 respectively.
- Create a payoff table with the five actions (remember that you can
combine purchases from more than one dealer and some plans don't make any
sense when the demand is considered) and four states of nature (demand)
- Create the opportunistic loss (regret) table.
- For each decision criteria (expected value, maximax, maximin, minimax),
find the payoff or loss for each action and the best action.
Project 4, Chapter 9
Part I - Markov Chain (10 points)
The Central Illinois Regional Airport (CIRA) in Bloomington-Normal is served by American Airlines, Delta, Allegiant, and Frontier. Of these, only American Airlines and Delta have daily flight service, so we will consider only those two airlines in this analysis.
Trip Advisor has airline recommendations and ratings at http://www.tripadvisor.com/Airlines. Assume that if a customer would recommend an airline to someone that they will fly that airline again the next time they fly. If they would not recommend an airline to someone, then they will fly a competitor airline the next time they fly. Cost or destination is not a factor in choosing an airline.
John has recently started a new job in Bloomington that will require him to fly often. He has no previous experience flying, so he looks at the number of ratings each airline has received on Trip Advisor and randomly chooses an airline based on the relative frequency of ratings. Example: If American has received 250 ratings and Delta has received 175 ratings, then there is a 250/425 chance John will pick American and a 175/425 chance he will pick Delta for the initial flight.
- Draw a transition diagram and give the transition matrix for John's flights out of CIRA.
- What is the probability that John's initial flight will be with Delta?
- What is the probability that John's fourth flight will be with American Airlines?
- What is the long term probability that John will fly with Delta?
Part II - Absorbing Markov Chain (10 points)
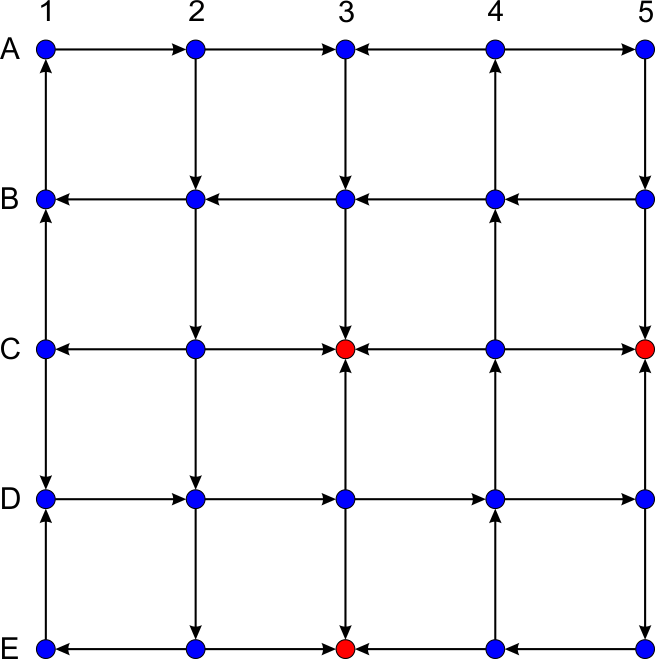 A 5×5 grid is laid out as shown in the figure to the right. Each node is labeled using a letter A-E for the row and a number 1-5 for the column. The top-left node would be A1, the bottom-right would be E5, while the center would be C3. The arrows indicate the direction of movement between nodes. Movement continues until reaching a node with no exit.
A 5×5 grid is laid out as shown in the figure to the right. Each node is labeled using a letter A-E for the row and a number 1-5 for the column. The top-left node would be A1, the bottom-right would be E5, while the center would be C3. The arrows indicate the direction of movement between nodes. Movement continues until reaching a node with no exit.
- Create a transition matrix in standard form.
- Find the fundamental matrix F.
- If you start at node C1, how many transitions can be expected before ending?
- If you start at node E5, how many transitions can be expected before ending?
- If you start at node A2, what is the probability of eventually ending up in cell C5?
- If the object is to take as many turns as possible, at which node(s) should you start?
- If the object is to end at cell C3, in which transient node(s) should you start?
Project 5, Chapter 10
Part I (10 points)
Consider the following two-person zero-sum game.
| |
Cereal |
Dairy |
Meat |
Snacks |
| Baking |
-3 |
1 |
-5 |
4 |
| Fruits |
2 |
-1 |
-2 |
3 |
| Pasta |
-1 |
1 |
3 |
-2 |
| Soda |
3 |
4 |
-1 |
2 |
The row player is "Rick's Ready Mart" and the column player is
"Corissa's Country Market".
Rick and Corissa own the only two grocery stores in town so that a sale
for Rick is a loss for Corissa and vice versa. Each week, they each run a
special on exactly one type of food in an effort to draw business into their
store. The matrix showing the choices and the gain in sales for Rick's store
are shown.
Answer the following questions.
- If Rick and Corissa each randomly select a food type to put on sale,
what are the strategies and what is the value of the game for Rick?
- What are the optimal strategies for Rick and Corissa? What is the value
of the game for Rick under that those strategies?
- Find the expected payoff values for each of Rick's actions if Corissa
plays her optimal strategies. Find the expected loss values for each of
Corissa's actions if Rick plays his optimal strategies.
- Rick finds out that Corissa is going to spin the spinner from the game
Life (10 slots) and place Cereal on sale if a 1 shows up, Dairy on sale if a
2 or 3 shows up, Meat on sale if a 4, 5, or 6 shows up, and Snacks on sale
if a 7, 8, 9, or 10 shows up.
- What is the expected value of each action for Rick?
- What should Rick's a priori strategy be using the expected value
criterion?
- What should Corissa's strategy really be (not what she said) if the
intent was to trick Rick into playing a particular strategy?
Part II (10 points)
- Create a 4 by 4 non-strictly determined game matrix with no recessive
rows or columns.
- Turn the matrix into a story problem. The matrix can be given as a
matrix, but come up with choices for the row and column players to make it
an interesting problem.
- Solve the game using the calculator.
 A 5×5 grid is laid out as shown in the figure to the right. Each node is labeled using a letter A-E for the row and a number 1-5 for the column. The top-left node would be A1, the bottom-right would be E5, while the center would be C3. The arrows indicate the direction of movement between nodes. Movement continues until reaching a node with no exit.
A 5×5 grid is laid out as shown in the figure to the right. Each node is labeled using a letter A-E for the row and a number 1-5 for the column. The top-left node would be A1, the bottom-right would be E5, while the center would be C3. The arrows indicate the direction of movement between nodes. Movement continues until reaching a node with no exit.