Stats: Correlation

Sum of Squares

We introduced a notation earlier in the course called the sum of squares. This notation was the SS notation, and will make these formulas much easier to work with.

Notice these are all the same pattern,

SS(x) could be written as

Also note that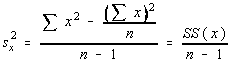

Pearson's Correlation Coefficient

There is a measure of linear correlation. The population parameter is denoted by the greek letter rho and the sample statistic is denoted by the roman letter r.

Here are some properties of r

• r only measures the strength of a linear relationship. There are other kinds of relationships besides linear.
• r is always between -1 and 1 inclusive. -1 means perfect negative linear correlation and +1 means perfect positive linear correlation
• r has the same sign as the slope of the regression (best fit) line
• r does not change if the independent (x) and dependent (y) variables are interchanged
• r does not change if the scale on either variable is changed. You may multiply, divide, add, or subtract a value to/from all the x-values or y-values without changing the value of r.
• r has a Student's t distribution

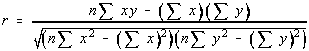Here is the formula for r. Don't worry about it, we won't be finding it this way. This formula can be simplified through some simple algebra and then some substitutions using the SS notation discussed earlier.

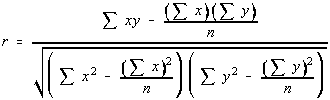If you divide the numerator and denominator by n, then you get something which is starting to hopefully look familiar. Each of these values have been seen before in the Sum of Squares notation section. So, the linear correlation coefficient can be written in terms of sum of squares.

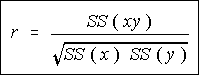This is the formula that we would be using for calculating the linear correlation coefficient if we were doing it by hand. Luckily for us, the TI-82 has this calculation built into it, and we won't have to do it by hand at all.

Hypothesis Testing

The claim we will be testing is "There is significant linear correlation"

The Greek letter for r is rho, so the parameter used for linear correlation is rho

• H₀: rho = 0
• H₁: rho <> 0

r has a t distribution with n-2 degrees of freedom, and the test statistic is given by:

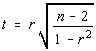
Now, there are n-2 degrees of freedom this time. This is a difference from before. As an over-simplification, you subtract one degree of freedom for each variable, and since there are 2 variables, the degrees of freedom are n-2.

This doesn't look like our

If you consider the standard error for r is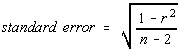

the formula for the test statistic is 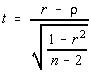, which does look like the pattern we're looking for.

Remember that

Hypothesis testing is always done under the assumption that the null hypothesis is true.

Since H₀ is rho = 0, this formula is equivalent to the one given in the book.
Additional Note: 1-r² is later identified as the coefficient of non-determination

Hypothesis Testing Revisited

If you are testing to see if there is significant linear correlation (a two tailed test), then there is another way to perform the hypothesis testing. There is a table of critical values for the Pearson's Product Moment Coefficient (PPMC) given in the text book. The degrees of freedom are n-2.

The test statistic in this case is simply the value of r. You compare the absolute value of r (don't worry if it's negative or positive) to the critical value in the table. If the test statistic is greater than the critical value, then there is significant linear correlation. Furthermore, you are able to say there is significant positive linear correlation if the original value of r is positive, and significant negative linear correlation if the original value of r was negative.

This is the most common technique used. However, the first technique, with the t-value must be used if it is not a two-tail test, or if a different level of significance (other than 0.01 or 0.05) is desired.

Causation

If there is a significant linear correlation between two variables, then one of five situations can be true.

• There is a direct cause and effect relationship
• There is a reverse cause and effect relationship
• The relationship may be caused by a third variable
• The relationship may be caused by complex interactions of several variables
• The relationship may be coincidental